题目内容
已知△ABC∽△DEF,且△ABC中BC边的高为4,△DEF中EF边上的高为9,则△ABC与△DEF这两个三角形的周长之比为 .
考点:相似三角形的性质
专题:探究型
分析:先求出两三角形的形的相似比,再根据相似三角形周长的比等于相似比即可得出结论.
解答:解:∵△ABC∽△DEF,且△ABC中BC边的高为4,△DEF中EF边上的高为9,
∴两三角形的相似比=
=
,
∴△ABC与△DEF这两个三角形的周长之比为
.
故答案为:
.
∴两三角形的相似比=
| 4 |
| 9 |
| 2 |
| 3 |
∴△ABC与△DEF这两个三角形的周长之比为
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查的是相似三角形的性质,即相似三角形对应高线的比、周长的比等于相似比.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
一辆汽车沿倾斜角α的斜坡前进800米,则它上升的高度是( )
| A、800•sinα米 | ||
B、
| ||
| C、800•cosα米 | ||
D、
|
 已知:如图,D是△ABC的边AB上一点,∠B+∠BCF=180°,DF交AC于点E,点E为DF中点.求证:AE=CE.
已知:如图,D是△ABC的边AB上一点,∠B+∠BCF=180°,DF交AC于点E,点E为DF中点.求证:AE=CE. 如图,矩形ABCD中,P是AB上一点,将矩形ABCD沿PD折叠,点A恰好落BC边上E点处,若DE=3PE,CD=9,则CE的长为
如图,矩形ABCD中,P是AB上一点,将矩形ABCD沿PD折叠,点A恰好落BC边上E点处,若DE=3PE,CD=9,则CE的长为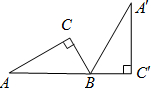 如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,求斜边AB旋转到A′B所扫过的扇形面积.
如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,求斜边AB旋转到A′B所扫过的扇形面积.