题目内容
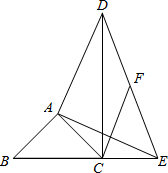
 已知△ABC中,AB=AC,以AB为直径的⊙O1分别交AC、BC于两D、E点,过B点的切线交OE的延长线于点F,连FD、BD、OD,下列结论:①四边形ODCE是平行四边形;②E是△BFD的内心;③E是△FDO的外心;④∠C=∠BFD;其中正确的有( )个.
已知△ABC中,AB=AC,以AB为直径的⊙O1分别交AC、BC于两D、E点,过B点的切线交OE的延长线于点F,连FD、BD、OD,下列结论:①四边形ODCE是平行四边形;②E是△BFD的内心;③E是△FDO的外心;④∠C=∠BFD;其中正确的有( )个.| A、1 | B、2 | C、3 | D、4 |
考点:三角形的内切圆与内心,等腰三角形的性质,平行四边形的判定,三角形的外接圆与外心,切线的性质
专题:
分析:首先利用三角形的中位线定理证明OE∥AC,然后证得△FDO≌△FBO,可以得到DF是圆的切线,然后利用内心以及外心的定义和的等腰三角形的性质:等边对等角即可作出判断.
解答: 解:连接AE,
解:连接AE,
∵AB是直径,
∴AE⊥BC,
又∵AB=AC,
∴BE=CE,
又∵OA=OB,
∴OE∥AC,
∴∠BOE=∠BAC,∠EOD=∠ADO,
∵∠BAC=∠ADO,
∴∠BOE=∠EOD,
在△FDO和△FBO中
∵
,
∴△FDO≌△FBO
∴∠ODF=∠OBF=90°,
即△FDO是直角三角形,DF是圆的切线.
如果四边形ODCE是平行四边形,则OD∥BC,则∠BEO=∠EOB=∠DOE
则△OBE是等边三角形,从而得到△ABC是等边三角形,与已知不符,故①是错误的;
∵FD、FB是圆的切线,
∴FD=FB,
又∵OB=OD
∴OF是BD的中垂线,
∴
=
,E在∠DFB的平分线上,
∴E在∠FBD的平分线上,
则E是△BFD的内心,故②正确;
Rt△DOF中,若E是△FDO的外心,则E是OF的中点,可以得到△ODE是等边三角形,则△ABC是等边三角形,与已知不符,故③是错误的;
设∠C=x°,则∠A=180-2x°,
则在直角△ABD中,∠ABD=90°-(180-2x)=2x-90°,
∵BF是切线,则∠ABF=90°,
∴∠DBF=90°-∠ABD=90°-(2x-90)°=180-2x°,
在等腰△BDF中,∠F=180°-2∠DBF=180°-2(180-2x)°=4x-180°,
而4x-180与x不一定相等,故④不正确.
故正确的只有②.
故选A.
 解:连接AE,
解:连接AE,∵AB是直径,

∴AE⊥BC,
又∵AB=AC,
∴BE=CE,
又∵OA=OB,
∴OE∥AC,
∴∠BOE=∠BAC,∠EOD=∠ADO,
∵∠BAC=∠ADO,
∴∠BOE=∠EOD,
在△FDO和△FBO中
∵
|
∴△FDO≌△FBO
∴∠ODF=∠OBF=90°,
即△FDO是直角三角形,DF是圆的切线.

如果四边形ODCE是平行四边形,则OD∥BC,则∠BEO=∠EOB=∠DOE
则△OBE是等边三角形,从而得到△ABC是等边三角形,与已知不符,故①是错误的;
∵FD、FB是圆的切线,
∴FD=FB,
又∵OB=OD
∴OF是BD的中垂线,
∴
 |
| DE |
 |
| BE |
∴E在∠FBD的平分线上,
则E是△BFD的内心,故②正确;
Rt△DOF中,若E是△FDO的外心,则E是OF的中点,可以得到△ODE是等边三角形,则△ABC是等边三角形,与已知不符,故③是错误的;
设∠C=x°,则∠A=180-2x°,
则在直角△ABD中,∠ABD=90°-(180-2x)=2x-90°,
∵BF是切线,则∠ABF=90°,
∴∠DBF=90°-∠ABD=90°-(2x-90)°=180-2x°,
在等腰△BDF中,∠F=180°-2∠DBF=180°-2(180-2x)°=4x-180°,
而4x-180与x不一定相等,故④不正确.
故正确的只有②.
故选A.
点评:此题主要考查了三角形的内心、外心以及切线的判定,解答的关键是正确证得DF是圆的切线.

练习册系列答案
相关题目
若数n=
,则数n3中含有数字9的个数是( )
| ||
| 20个9 |
| A、39 | B、37 | C、34 | D、31 |
 已知:如图,在△ABC中,∠BAC=90°,AB=AC,点E在边BC的延长线上,DA⊥AE,AD=AE.
已知:如图,在△ABC中,∠BAC=90°,AB=AC,点E在边BC的延长线上,DA⊥AE,AD=AE. 已知:如图,D是△ABC的边AB上一点,∠B+∠BCF=180°,DF交AC于点E,点E为DF中点.求证:AE=CE.
已知:如图,D是△ABC的边AB上一点,∠B+∠BCF=180°,DF交AC于点E,点E为DF中点.求证:AE=CE.