题目内容
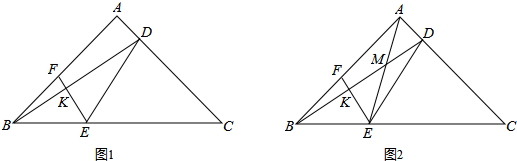
1.如图,在△ABC中,AB=AC,∠A=90°,点D为AC上一点,连接BD,在边BC上取点E,使∠EDC=∠ADB,过E作EF⊥BD于K,交直线AB于F.(1)如图①,求证:BF=2AD;
(2)如图②,在(1)的条件下,连接AE.交BD于M,若ED=2EF,请您探究线段AM与ME之间的数量关系,并证明您的结论.
分析 (1)作BG∥AC,交DE延长线于G点,作DH⊥BG,交BG于H;然后判断出△BEF≌△BEG,可得BF=BG,再判断出△DBG是等腰三角形,四边形ABHD是矩形,所以AD=BH=$\frac{1}{2}$BG=$\frac{1}{2}$BF,因此BF=2AD;
(2)如图,作EN∥BG,交BD于N,因为△BEF≌△BEG,所以EF=EG,然后根据ED=2EF,可得ED=2EG;再判断出EN与AD的关系,即可判断出AM与ME之间的数量关系.
解答 (1)证明:如图,作BG∥AC,交DE延长线于G点,作DH⊥BG,交BG于H.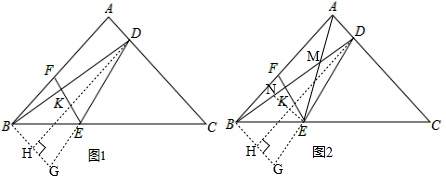
∵EF⊥BD,
∴∠BFE=∠ADB=∠DBG=∠EDC.
∵∠G=∠EDC,
∴∠DBG=∠BFE=∠G.
∵∠EBF=∠EBG=45°,
∴△BEF≌△BEG,BF=BG.
∵∠DBG=∠G,
∴DB=DG.
∵DH⊥BG,
∴BH=GH.
∵BG∥AC,
∴ABHD是矩形,
∴AD=BH=$\frac{1}{2}$BG=$\frac{1}{2}$BF.
∴BF=2AD.
(2)如图,作EN∥BG,交BD于N,
∵△BEF≌△BEG,
∴EF=EG.
∵ED=2EF,∴ED=2EG.
∴$\frac{EN}{BG}=\frac{DE}{DG}=\frac{2}{3}$,BG=2AD,
∴$\frac{EN}{AD}=\frac{2×2}{3}=\frac{4}{3}$,
∴$\frac{AM}{ME}=\frac{AD}{EN}=\frac{3}{4}$.
点评 此题主要考查了全等三角形的判定与性质,要熟练掌握,解答此题的关键是判断出:△BEF≌△BEG.

练习册系列答案
相关题目