题目内容
11.A(3,0)是以O为原点的平面直角坐标系中的一点,把线段OA绕点O逆时针旋转90°,得线段OB,则点B的坐标为(0,3).分析 先根据点A的坐标求出OA的长度,根据旋转变换只改变图形的位置,不改变图形的形状与大小得到OB=OA,再根据平面直角坐标系写出点B的坐标即可.
解答  解:∵点A的坐标为(3,0),
解:∵点A的坐标为(3,0),
∴OA=3,
∵线段OA绕点O逆时针旋转90°得到线段OB,
∴OB=OA=3,
∴点B的坐标为(0,3).
故答案为:(0,3).
点评 本题考查了坐标与图形变化-旋转,根据旋转变换只改变图形的位置,不改变图形的形状与大小求出OB的长度是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
6.将平面直角坐标系中的点P(-2,3),绕坐标原点O顺时针旋转90°,到达点P′,则点P′的坐标是( )
| A. | (2,3) | B. | (2,-3) | C. | (-3,-2) | D. | (3,2) |
1.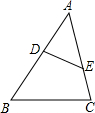 如图,点D、E分别在线段AB、AC上且∠ABC=∠AED,若DE=4,AE=5,BC=8,则AB的长为( )
如图,点D、E分别在线段AB、AC上且∠ABC=∠AED,若DE=4,AE=5,BC=8,则AB的长为( )
 如图,点D、E分别在线段AB、AC上且∠ABC=∠AED,若DE=4,AE=5,BC=8,则AB的长为( )
如图,点D、E分别在线段AB、AC上且∠ABC=∠AED,若DE=4,AE=5,BC=8,则AB的长为( )| A. | $\frac{5}{2}$ | B. | 10 | C. | $\frac{2}{5}$ | D. | $\frac{1}{10}$ |
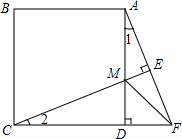 已知,如图在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,求证:∠MFD=45°.
已知,如图在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,求证:∠MFD=45°.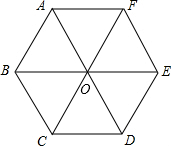 如图,正六边形ABCDEF是由边长为2厘米的六个等边三角形拼成,那么图中
如图,正六边形ABCDEF是由边长为2厘米的六个等边三角形拼成,那么图中
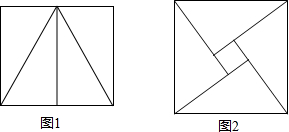 小华和小明分别用4个全等的直角三角形拼图:小华拼成的矩形(图1)的周长为20cm,小明拼成的正方形(图2)中有一边长为1cm的正方形小孔,则小明拼成的正方形的周长
小华和小明分别用4个全等的直角三角形拼图:小华拼成的矩形(图1)的周长为20cm,小明拼成的正方形(图2)中有一边长为1cm的正方形小孔,则小明拼成的正方形的周长