题目内容
17.AD是△ABC的边BC上的中线,AB=6,AC=4,则边BC的取值范围是2<BC<10,中线AD的取值范围是1<AD<5.分析 根据三角形的三边关系定理求出BC的范围即可;延长AD到E,使AD=DE,连接BE,证三角形全等,推出BE=AC=6,在三角形ABE中,根据三角形的三边关系定理求出即可.
解答 解:∵在△ABC中,AB=6,AC=4,
∴6-4<BC<6+4,
∴2<BC<10;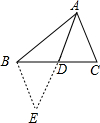 延长AD到E,使AD=DE,连接BE,如图所示:
延长AD到E,使AD=DE,连接BE,如图所示:
∵AD为中线,
∴BD=DC,
在△ADC和△EDB中,$\left\{\begin{array}{l}{AD=DE}\\{∠ADC=∠BDE}\\{CD=BD}\end{array}\right.$,
∴△ADC≌△EDB(SAS),
∴AC=BE=4,
在△ABE中,AB=6,BE=4,
∴6-4<AE<6+4,
∴2<2AD<10,
∴1<AD<5,
故答案为:2<BC<10,1<AD<5.
点评 本题主要考查了全等三角形的性质和判定、三角形的三边关系定理的应用等知识,通过作辅助线构建三角形全等是解决问题的关键.

练习册系列答案
相关题目
7. 如图,△ABC 中,∠C=3∠BAC,边CB的延长线与外角∠EAB的平分线交于点D.若AD=AB,则∠BAC的度数是( )
如图,△ABC 中,∠C=3∠BAC,边CB的延长线与外角∠EAB的平分线交于点D.若AD=AB,则∠BAC的度数是( )
 如图,△ABC 中,∠C=3∠BAC,边CB的延长线与外角∠EAB的平分线交于点D.若AD=AB,则∠BAC的度数是( )
如图,△ABC 中,∠C=3∠BAC,边CB的延长线与外角∠EAB的平分线交于点D.若AD=AB,则∠BAC的度数是( )| A. | 12° | B. | 15° | C. | 30° | D. | 10° |
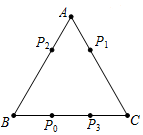 如图,电子跳蚤游戏盘是如图所示的△ABC,AB=BC=AC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与点P2013之间的距离为( )
如图,电子跳蚤游戏盘是如图所示的△ABC,AB=BC=AC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与点P2013之间的距离为( ) (1)如图,在方格纸中先通过向上平移4个单位长,由图形A得到图形B,再由图形B先向右平移4个单位长度(怎样平移),再绕点P2顺时针旋转90°(怎样旋转)得到图形C(对于平移变换要求回答出平移的方向和平移的距离;对于旋转变换要求回答出旋转中心、旋转方向和旋转角度);
(1)如图,在方格纸中先通过向上平移4个单位长,由图形A得到图形B,再由图形B先向右平移4个单位长度(怎样平移),再绕点P2顺时针旋转90°(怎样旋转)得到图形C(对于平移变换要求回答出平移的方向和平移的距离;对于旋转变换要求回答出旋转中心、旋转方向和旋转角度); 已知一次函数y=kx+b的图象经过点A(-3,-2)及点B(-1,2).
已知一次函数y=kx+b的图象经过点A(-3,-2)及点B(-1,2).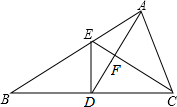 △ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.
△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.
 如图所示,在正方形ABCD的边CB的延长线上取点F,连结AF,在AF上取点G,使得AG=AD,连结DG,过点A作AE⊥AF,交DG于点E.
如图所示,在正方形ABCD的边CB的延长线上取点F,连结AF,在AF上取点G,使得AG=AD,连结DG,过点A作AE⊥AF,交DG于点E.