题目内容
12. 已知一次函数y=kx+b的图象经过点A(-3,-2)及点B(-1,2).
已知一次函数y=kx+b的图象经过点A(-3,-2)及点B(-1,2).(1)求此一次函数的解析式,并画出图象;
(2)求此函数图象与两坐标轴所围成的三角形的面积.
分析 (1)根据点A、B的坐标利用待定系数法即可求出直线AB的解析式,再在坐标系中标出点A、B,连点成线即可画出一次函数的图象;
(2)设直线AB与x轴交点为C,与y轴交点为D,分别将y=0、x=0代入函数解析式中求出点C、D的坐标,再根据三角形的面积公式即可得出此函数图象与两坐标轴所围成的三角形的面积.
解答 解:(1)将A(-3,-2)、B(-1,2)代入y=kx+b中,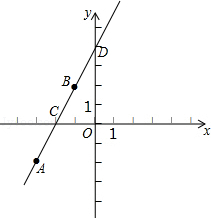
$\left\{\begin{array}{l}{-3k+b=-2}\\{-k+b=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=4}\end{array}\right.$,
∴此一次函数的解析式为y=2x+4.
描出点A、B,连点成线,画出函数图象如图所示.
(2)设直线AB与x轴交点为C,与y轴交点为D,
当y=2x+4=0时,x=-2,
∴点C(-2,0);
当x=0时,y=4,
∴点D(0,4).
∴OC=2,OD=4,
∴S△COD=$\frac{1}{2}$OC•OD=$\frac{1}{2}$×2×4=4.
点评 本题考查了待定系数法求一次函数解析式、一次函数的图象、三角形的面积以及一次函数图象上点的坐标特征,解题的关键是:(1)根据点A、B的坐标利用待定系数法求出函数解析式;(2)根据一次函数图象上点的坐标特征求出直线AB与x、y轴的交点坐标.

练习册系列答案
相关题目
3.某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如表:[增加的辆数为正数,减少的辆数为负数]
(1)本周星期六生产多少摩托车?
(2)产量最多的那天比产量最少的那天多生产多少辆?
(3)本周实际总产量为多少辆?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(2)产量最多的那天比产量最少的那天多生产多少辆?
(3)本周实际总产量为多少辆?
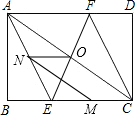 矩形ABCD中,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F,连接EF,点M为EC的中点,N点为AE上的一个动点,AB=6
矩形ABCD中,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F,连接EF,点M为EC的中点,N点为AE上的一个动点,AB=6 如图,⊙O是等腰三角形ABC的外接圆,AB=AC,∠A=45°,BD为⊙O的直径,连结CD,则∠DBA=22.5°.
如图,⊙O是等腰三角形ABC的外接圆,AB=AC,∠A=45°,BD为⊙O的直径,连结CD,则∠DBA=22.5°.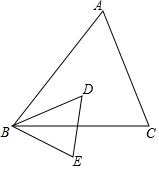 如图,在△ABC和△DBE中,$\frac{AB}{DB}$=$\frac{BC}{BE}$=$\frac{5}{3}$,且∠DBA=∠CBE.
如图,在△ABC和△DBE中,$\frac{AB}{DB}$=$\frac{BC}{BE}$=$\frac{5}{3}$,且∠DBA=∠CBE.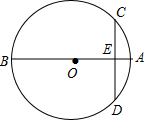 ⊙O的两条弦AB,CD相交于点E.
⊙O的两条弦AB,CD相交于点E.