题目内容
14.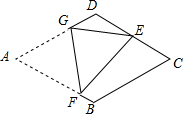 如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则cos∠EFG的值为$\frac{\sqrt{21}}{7}$.
如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则cos∠EFG的值为$\frac{\sqrt{21}}{7}$.
分析 作EH⊥AD于H,连接BE、BD,连接AE交FG于O,如图,利用菱形的性质得△BDC为等边三角形,∠ADC=120°,再在在Rt△BCE中计算出BE=$\sqrt{3}$CE=$\sqrt{3}$,接着证明BE⊥AB,设AF=x,利用折叠的性质得到EF=AF,FG垂直平分AE,∠EFG=∠AFG,所以在Rt△BEF中利用勾股定理得(2-x)2+($\sqrt{3}$)2=x2,解得x=$\frac{7}{4}$,接下来计算出AE,从而得到OA的长,然后在Rt△AOF中利用勾股定理计算出OF,再利用余弦的定义求解.
解答 解:作EH⊥AD于H,连接BE、BD,连接AE交FG于O,如图,
∵四边形ABCD为菱形,∠A=60°,
∴△BDC为等边三角形,∠ADC=120°,
∵E点为CD的中点,
∴CE=DE=1,BE⊥CD,
在Rt△BCE中,BE=$\sqrt{3}$CE=$\sqrt{3}$,
∵AB∥CD,
∴BE⊥AB,
设AF=x,
∵菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,
∴EF=AF,FG垂直平分AE,∠EFG=∠AFG,
在Rt△BEF中,(2-x)2+($\sqrt{3}$)2=x2,解得x=$\frac{7}{4}$,
在Rt△DEH中,DH=$\frac{1}{2}$DE=$\frac{1}{2}$,HE=$\sqrt{3}$DH=$\frac{\sqrt{3}}{2}$,
在Rt△AEH中,AE=$\sqrt{(2+\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=$\sqrt{7}$,
∴AO=$\frac{\sqrt{7}}{2}$,
在Rt△AOF中,OF=$\sqrt{(\frac{7}{4})^{2}-(\frac{\sqrt{7}}{2})^{2}}$=$\frac{\sqrt{21}}{4}$,
∴cos∠AFO=$\frac{\frac{\sqrt{21}}{4}}{\frac{7}{4}}$=$\frac{\sqrt{21}}{7}$.
故答案为$\frac{\sqrt{21}}{7}$.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了菱形的性质.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案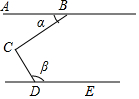
| A. | ∠α+∠β=180° | B. | ∠β-∠α=90° | C. | ∠β=3∠α | D. | ∠α+∠β=90° |
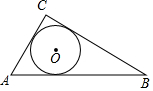 如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
如图,⊙O是△ABC的内切圆,则点O是△ABC的( )| A. | 三条边的垂直平分线的交点 | B. | 三条角平分线的交点 | ||
| C. | 三条中线的交点 | D. | 三条高的交点 |
 如图表示下列四个不等式组中其中一个的解集,这个不等式组是( )
如图表示下列四个不等式组中其中一个的解集,这个不等式组是( )| A. | $\left\{\begin{array}{l}{x≥2}\\{x>-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≤2}\\{x<-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥2}\\{x<-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≤2}\\{x>-3}\end{array}\right.$ |
| A. | a4•a | B. | (a2)2 | C. | a3+a3 | D. | a4÷a |
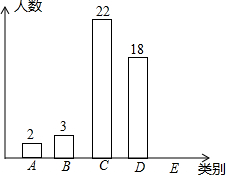 某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).
某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8). 如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长与BC的延长线交于点E.求证:BC=CE.
如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长与BC的延长线交于点E.求证:BC=CE.