题目内容
8.下列多项式乘法,能用平方差公式计算的是( )| A. | (-3x-2)(3x+2) | B. | (-a-b)(-b+a) | C. | (-3x+2)(2-3x) | D. | (3x+2)(2x-3) |
分析 根据平方差公式对各选项进行逐一分析即可.
解答 解:A、原式可化为-(3x+2)(3x+2),不能用平方差公式计算,故本选项错误;
B、原式可化为-(a+b)(a-b),能用平方差公式计算,故本选项正确;
C、原式可化为(2-3x)(2-3x),不能用平方差公式计算,故本选项错误;
D、不符合两个数的和与这两个数的差相乘,不能用平方差公式计算,故本选项错误.
故选B.
点评 本题考查的是平方差公式,熟知两个数的和与这两个数的差相乘,等于这两个数的平方差是解答此题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
18.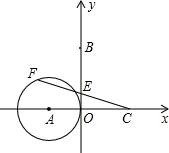 如图,在平面直角坐标系中,A(-5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )
如图,在平面直角坐标系中,A(-5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )
 如图,在平面直角坐标系中,A(-5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )
如图,在平面直角坐标系中,A(-5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )| A. | $\frac{160}{3}$ | B. | 40 | C. | 20 | D. | $\frac{40}{3}$ |
13.若把分式$\frac{x+3y}{2x}$的x、y同时扩大为原来的2倍,则分式的值( )
| A. | 扩大2倍 | B. | 缩小2倍 | C. | 不变 | D. | 缩小3倍 |
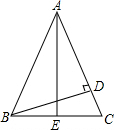 如图,△ABC中,AB=AC,E为BC中点,BD⊥AC,垂足为D,∠EAD=25°.求:∠ABD.
如图,△ABC中,AB=AC,E为BC中点,BD⊥AC,垂足为D,∠EAD=25°.求:∠ABD.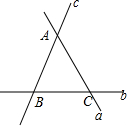 如图,直线a,b,c两两相交于A,B,C三点,则图中有6对对顶角;有12对同位角;有6对内错角;有6对同旁内角.
如图,直线a,b,c两两相交于A,B,C三点,则图中有6对对顶角;有12对同位角;有6对内错角;有6对同旁内角. 在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公共点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是b>2或b<-2.
在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公共点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是b>2或b<-2.