题目内容
18.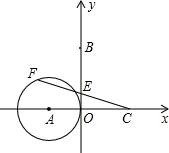 如图,在平面直角坐标系中,A(-5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )
如图,在平面直角坐标系中,A(-5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )| A. | $\frac{160}{3}$ | B. | 40 | C. | 20 | D. | $\frac{40}{3}$ |
分析 当FC与⊙A相切且位于x轴下方时,△BCE的面积有最大值,由切线的性质可知△AFC为直角直角三角形,依据勾股定理可求得FC的长,然后证明△OEC∽△FAC,由相似三角形的性质可求得OE的长,从而得到BE的长,最后依据三角形的面积公式求解即可.
解答 解:如图所示:当CF与⊙A相切时,△BCE的面积有最大值.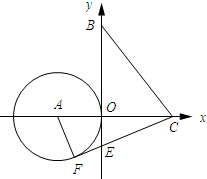
∵CF与⊙A相切,
∴AF⊥FC.
∴△AFC为直角三角形.
∴FC=$\sqrt{A{C}^{2}-A{F}^{2}}$=12.
∵∠AFC=∠EOC,∠OCE=∠FCA,
∴△OEC∽△FAC.
∴$\frac{OE}{AF}=\frac{OC}{CF}$,即$\frac{OE}{5}=\frac{8}{12}$,解得;OE=$\frac{10}{3}$.
∴BE=OB+OE=10+$\frac{10}{3}$=$\frac{40}{3}$.
∴△CBE面积的最大值=$\frac{1}{2}$BE•OC=$\frac{1}{2}$×$\frac{40}{3}$×8=$\frac{160}{3}$.
故选;A.
点评 本题主要考查的是圆的综合应用,解答本题主要应用了切线的性质、勾股定理、相似三角形的性质和判定、三角形的面积公式,找出△EBC取得最大值的条件是解题的关键.

练习册系列答案
相关题目
6. 如图,在?ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
如图,在?ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
 如图,在?ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
如图,在?ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 8cm |
7.如图中,∠1和∠2不是同旁内角的是( )
| A. |  | B. |  | C. |  | D. |  |
8.下列多项式乘法,能用平方差公式计算的是( )
| A. | (-3x-2)(3x+2) | B. | (-a-b)(-b+a) | C. | (-3x+2)(2-3x) | D. | (3x+2)(2x-3) |
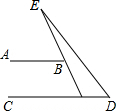 如图所示,AB∥CD,∠ABE=66°,∠D=54°,则∠E的度数为12°.
如图所示,AB∥CD,∠ABE=66°,∠D=54°,则∠E的度数为12°.