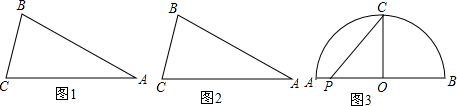
题目内容
13.反比例函数是中考常考内容,小明遇到两道关于反比例函数知识的难题,请你帮他解答.(1)如图1,已知反比例函数y=$\frac{{k}_{1}}{2x}$的图象与一次函数y=k2x+b的图象交于A,B两点,A(1,n),B(-,-2).
①求反比例函数和一次函数的解析式;
②在x轴上是否存在点P,使△AOP为等腰三角形?若存在,请你直接写出P点的坐标;若不存在,请说明理由.
(2)如图2,正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.
①求反比例函数的解析式;
②如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.
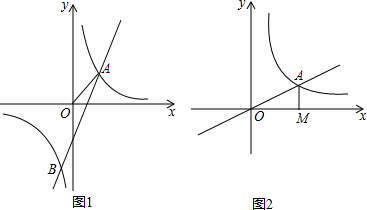
分析 (1)①先把点B的坐标代入反比例函数解析式,求出k1的值即可得出其解析式,再求出点A的坐标,再把A、B两点坐标代入一次函数即可得出其解析式;
②分OA=OP,OA=AP及OP=AP三种情况进行分类讨论即可;
(2)①设A点的坐标为(a,b),则b=$\frac{k}{a}$,再由△OAM的面积为1可得出k的值,进而可得出其解析式;
②根据题意画出图形,利用待定系数法求出直线BC的解析式,再令y=0求出x的值即可得出P点坐标.
解答 解:(1)①∵点B(-$\frac{1}{2}$,-2)在反比例函数y=$\frac{{k}_{1}}{2x}$的图象上,
∴-2=$\frac{{k}_{1}}{2×(-\frac{1}{2})}$,
∴k1=2.
∴反比例函数的解析式为y=$\frac{1}{x}$,
又∵A(1,n)在反比例函数图象上,
∴n=$\frac{1}{1}$,
∴n=1;
∴A点坐标为(1,1);
∴一次函数y=k2x+b的图象经过点A(1,1),B(-,-2);
∴$\left\{\begin{array}{l}{k}_{2}+b=1\\-\frac{1}{2}+b=-2\end{array}\right.$,
∴$\left\{\begin{array}{l}{k}_{2}=2\\ b=-1\end{array}\right.$,
∴一次函数的解析式为y=2x-1;
②存在符合条件的点P.
若OA=OP,则P($\sqrt{2}$,0)或(-$\sqrt{2}$,0),
若AP=OA,则P(2,0),
若OP=AP,则(1,0),
故点P的坐标为($\sqrt{2}$,0),(-$\sqrt{2}$,0),(2,0),(1,0);
(2)①设A点的坐标为(a,b),则b=$\frac{k}{a}$,
∴ab=k.
∵$\frac{1}{2}$ab=1,
∴$\frac{1}{2}$k=1,
∴k=2,
∴反比例函数的解析式为y=$\frac{2}{x}$. ②根据题意画出图形,如图所示:
②根据题意画出图形,如图所示:
联立得$\left\{\begin{array}{l}y=\frac{2}{x}\\ y=\frac{1}{2}x\end{array}\right.$,解得$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$,
∴A为(2,1).
设A点关于x轴的对称点为C,则C点的坐标为(2,-1).
令直线BC的解析式为y=mx+n
∵B为(1,2),
将B和C的坐标代入得:$\left\{\begin{array}{l}2m+n=-1\\ m+n=2\end{array}\right.$,解得:$\left\{\begin{array}{l}m=-3\\ n=5\end{array}\right.$,
∴BC的解析式为y=-3x+5.
当y=0时,x=$\frac{5}{3}$,
∴P点为($\frac{5}{3}$,0).
点评 本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点、待定系数法求一次函数的解析式及等腰三角形的性质等知识,难度适中.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | y=2(x+1)2+3 | B. | y=-x2+4x+1 | C. | y=2x2+4x-3 | D. | y=-2x2-x+5 |
| A. | 4.16×1012 | B. | 4.16×1013 | C. | 0.416×1012 | D. | 416×1010 |
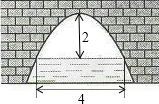 如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )
如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )| A. | 3 | B. | 2$\sqrt{6}$ | C. | 3$\sqrt{2}$ | D. | 2 |
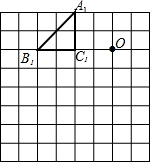 如图,网格图中每一小格的边长都相等.
如图,网格图中每一小格的边长都相等.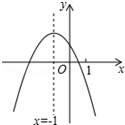 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论: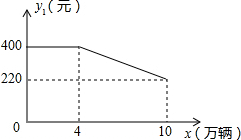 “低碳生活”作为一种健康、环保、安全的生活方式,受到越来越多人的关注.某公司生产的健身自行车在市场上受到普遍欢迎,在国内市场和国外市场畅销,生产的产品可以全部售出,在国内市场每辆的利润y1(元)与销量x(万辆)的关系如图所示;在国外市场每辆的利润y2 (元)与销量x(万量)的关系为:
“低碳生活”作为一种健康、环保、安全的生活方式,受到越来越多人的关注.某公司生产的健身自行车在市场上受到普遍欢迎,在国内市场和国外市场畅销,生产的产品可以全部售出,在国内市场每辆的利润y1(元)与销量x(万辆)的关系如图所示;在国外市场每辆的利润y2 (元)与销量x(万量)的关系为: