题目内容
3.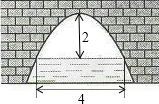 如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )
如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )| A. | 3 | B. | 2$\sqrt{6}$ | C. | 3$\sqrt{2}$ | D. | 2 |
分析 根据已知得出直角坐标系,进而求出二次函数解析式,再通过把y=-1代入抛物线解析式得出水面宽度,即可得出答案.
解答 解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
设顶点式y=ax2+2,代入A点坐标(-2,0),
得出:a=-0.5,
所以抛物线解析式为y=-0.5x2+2,
当水面下降1米,通过抛物线在图上的观察可转化为:
当y=-1时,对应的抛物线上两点之间的距离,也就是直线y=-1与抛物线相交的两点之间的距离,
可以通过把y=-1代入抛物线解析式得出:
-1=-0.5x2+2,
解得:x=±$\sqrt{6}$,
所以水面宽度增加到2$\sqrt{6}$米,
故选:B.
点评 此题主要考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键.

练习册系列答案
相关题目
18.上学期,为创建文明城市,29中举行“社会主义核心价值观”演讲比赛,比赛聘请了10位老师和10位学生担任评委,其中九(7)班的得分情况如下面的统计图(表)所示:
老师评委计分统计表
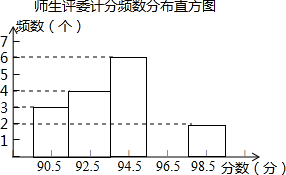
(1)在频数分布直方图中,自左向右第四组的频数为5.
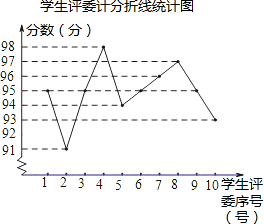
(2)学生评委计分的中位数是95分.
(3)计算最后得分的规定如下:在评委的计分中各去掉一个最高分、一个最低分,分别计算平均数(老师、学生评委分开计算);并且按老师、学生评委的平均分各占60%、40%的方法计算各班最后得分,已知九(7)班最后得分为94.4分,求统计表中x的值.
老师评委计分统计表
| 评委序号/号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 计分/分 | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |


(1)在频数分布直方图中,自左向右第四组的频数为5.
(2)学生评委计分的中位数是95分.
(3)计算最后得分的规定如下:在评委的计分中各去掉一个最高分、一个最低分,分别计算平均数(老师、学生评委分开计算);并且按老师、学生评委的平均分各占60%、40%的方法计算各班最后得分,已知九(7)班最后得分为94.4分,求统计表中x的值.
12.设x是有理数,那么下列各式中一定表示正数的是( )
| A. | 2015x | B. | x+2015 | C. | |2015x| | D. | |x|+2015 |
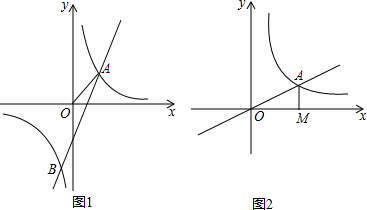
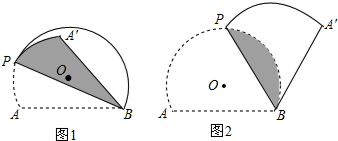
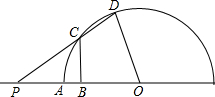 已知如图半圆O的半径OA=4,P是OA延长线上一点,过线段OP的中点B作垂线交⊙O于点C,射线PC交⊙O于点D,联结OD.
已知如图半圆O的半径OA=4,P是OA延长线上一点,过线段OP的中点B作垂线交⊙O于点C,射线PC交⊙O于点D,联结OD. 如图,已知线段a,b,c.(尺规作图,保留作图痕迹,不写做法)
如图,已知线段a,b,c.(尺规作图,保留作图痕迹,不写做法)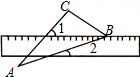 将一把有刻度的直尺摆放在含30°角的三角板(∠A=30°,∠C=90°)上,其中顶点B在直尺的一边上,已知∠1=55°,则∠2=25度.
将一把有刻度的直尺摆放在含30°角的三角板(∠A=30°,∠C=90°)上,其中顶点B在直尺的一边上,已知∠1=55°,则∠2=25度.