题目内容
18.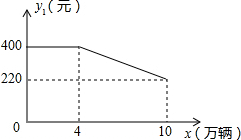 “低碳生活”作为一种健康、环保、安全的生活方式,受到越来越多人的关注.某公司生产的健身自行车在市场上受到普遍欢迎,在国内市场和国外市场畅销,生产的产品可以全部售出,在国内市场每辆的利润y1(元)与销量x(万辆)的关系如图所示;在国外市场每辆的利润y2 (元)与销量x(万量)的关系为:
“低碳生活”作为一种健康、环保、安全的生活方式,受到越来越多人的关注.某公司生产的健身自行车在市场上受到普遍欢迎,在国内市场和国外市场畅销,生产的产品可以全部售出,在国内市场每辆的利润y1(元)与销量x(万辆)的关系如图所示;在国外市场每辆的利润y2 (元)与销量x(万量)的关系为:y2=$\left\{\begin{array}{l}-20x+360(0≤x≤6)\\ 240(4≤x≤10)\end{array}\right.$.
(1)求国内市场的销售总利润z1(万元)关于销售量x(万辆)的函数关系式,并指出自变量的取值范围.
(2)该公司的年生产能力为10万辆,请帮助该公司确定国内、国外市场的销量各为多少时,公司的年利润最大?
分析 (1)根据图表中的数据,设出关系式,代入数据即可求出关系式;
(2)题中等量关系为:总利润=国内利润+国外利润,根据等量关系函数表达式,分段讨论出最大值即可解决.
解答 解:(1)y1=$\left\{\begin{array}{l}400(0≤x≤4)\\-30x+520(4≤x≤10)\end{array}\right.$则Z1=xy=$\left\{\begin{array}{l}400x(0≤x≤4)\\-30{x^2}+520x(4≤x≤10)\end{array}\right.$
(2)该公司在国外市场的利润Z2=xy=$\left\{\begin{array}{l}-20{x^2}+360x(0≤x≤6)\\ 240x(6≤x≤10)\end{array}\right.$
该公司的年生产能力为10万辆,在国内市场销售t万辆时,在国外市场销售(10-t)万辆,则
Z1=$\left\{\begin{array}{l}400t(0≤t≤4)\\-30{t^2}+520t(4≤t≤10)\end{array}\right.$,
Z2=$\left\{\begin{array}{l}-20{(10-t)^2}+360(10-t)(0≤10-t≤6)\\ 240(10-t)(6≤10-t≤10)\end{array}\right.$=$\left\{\begin{array}{l}-20{t^2}+40t+1600(4≤t≤10)\\-240x+2400(0≤x≤4)\end{array}\right.$
设该公司每年的总利润为w(万元),则
W=Z1+Z2=$\left\{\begin{array}{l}160t+2400(0≤t≤4)\\-50{t^2}+560t+1600(4≤t≤10)\end{array}\right.$=$\left\{\begin{array}{l}160t+2400(0≤t≤4)\\-50{(t-\frac{28}{5})^2}+3168(4≤t≤10)\end{array}\right.$
当0≤t≤4时,w随t的增大而增大,当t=4时,w取最大值,此时w=3040.当4≤t≤10时,当t=$\frac{28}{5}$时,w取最大值,此时w=3168.综合得:当t=$\frac{28}{5}$时,w的最大值为3168.此时,国内的销量为$\frac{28}{5}$万辆,国外市场销量为$\frac{22}{5}$万辆,总利润为3168万元.
点评 此题考查了二次函数的应用,涉及的知识有:一次函数的图象与性质,二次函数的图象与性质,分段函数,以及待定系数法确定函数解析式,是一道综合性较强的应用题.

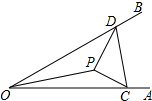 如图,∠AOB=30°,点P是∠AOB内的一个定点,OP=20cm,点C、D分别是OA、OB上的动点,连结CP、DP、CD,则△CPD周长的最小值为( )
如图,∠AOB=30°,点P是∠AOB内的一个定点,OP=20cm,点C、D分别是OA、OB上的动点,连结CP、DP、CD,则△CPD周长的最小值为( )| A. | 10cm | B. | 15cm | C. | 20cm | D. | 40cm |

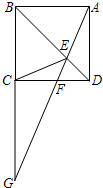 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F,则:①四边形ABCD是正方形;②△CEG∽△FEC;③C是BG的中点;④当AE=2EF时,FG=3EF,正确的有几个( )
如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F,则:①四边形ABCD是正方形;②△CEG∽△FEC;③C是BG的中点;④当AE=2EF时,FG=3EF,正确的有几个( ) 如图,已知线段a,b,c.(尺规作图,保留作图痕迹,不写做法)
如图,已知线段a,b,c.(尺规作图,保留作图痕迹,不写做法)