题目内容
4.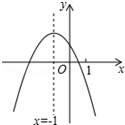 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②3b+2c<0;③m(am+b)<a-b;④ax2+bx+c<ax2+2ax-3a,
其中正确结论的是(填正确的序号)①②.
分析 利用二次函数图象的相关知识与函数系数的联系,需要根据图形,逐一判断.
解答 解:∵图象与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴b2-4ac>0,
∴4ac-b2<0,①正确;
∴-$\frac{b}{2a}$=-1,
∴b=2a,
∵a+b+c<0,
∴$\frac{1}{2}$b+b+c<0,3b+2c<0,
∴②是正确;
∵抛物线的对称轴是直线x=-1,
∴y=a-b+c的值最大,
把x=m代入得:y=am2+bm+c≤a-b+c,
∴am2+bm+b≤a,
即m(am+b)≤a-b,
∴③错误;
∵把x=1代入抛物线得:y=a+b+c<0,
∴2a+2b+2c<0,
∵b=2a,
∴ax2+bx+c<ax2+2ax-3a可化为c<-3a
即3a+c<0,
即3b+2c<0,由②知错误
∴④错误;
即正确为①②,
故选:①②.
点评 本题主要考查了二次函数图象与系数的关系,在解题时要注意二次函数的系数与其图象的形状,对称轴,特殊点的关系,也要掌握在图象上表示一元二次方程ax2+bx+c=0的解的方法,同时注意特殊点的运用.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 已知,如图,∠AEC=∠BFD,CE∥BF,求证:AB∥CD.
已知,如图,∠AEC=∠BFD,CE∥BF,求证:AB∥CD.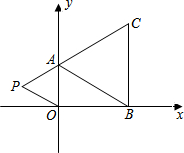 如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,c=2b-a
如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,c=2b-a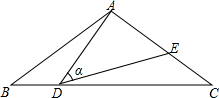 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$,则线段CE的最大值为6.4.
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$,则线段CE的最大值为6.4.