题目内容
10.①计算x2•x4=x6②已知am=2,an=3,那么a2m-n=$\frac{4}{3}$
③已知3n=a,3m=b,则3m+n+1=3ab.
④已知${3^m}=\frac{1}{81}$,则m=-4.
★⑤已知:(x+2)x+5=1,则x=-5或-1或-3.
分析 ①根据同底数幂的乘法法则进行计算即可;
②根据同底数幂的除法法则进行计算即可;
③根据同底数幂的乘法法则进行计算即可;
④把$\frac{1}{81}$化为3-4的形式即可得出结论;
⑤分x+5=0,x+2≠0;x+2=1或x+2=-1,x+5为偶数进行解答即可.
解答 解:①x2•x4=x2+4=x6.
故答案为:x6;
②∵am=2,an=3,
∴a2m-n=$\frac{{(a}^{m})^{2}}{{a}^{n}}$=$\frac{{2}^{2}}{3}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$;
③∵3n=a,3m=b,
∴3m+n+1=3n•3m•3=3ab.
故答案为:3ab;
④∵$\frac{1}{81}$=3-4,
∴m=-4.
故答案为:-4;
⑤当x+5=0,x+2≠0时,x=-5;
当x+2=1时,x=-1;
当x+2=-1,x+5为偶数时,x=-3.
故答案为:-5或-1或-3.
点评 本题考查的是同底数幂的除法,涉及到同底数幂的除法法则、幂的乘方与积的乘方法则、0指数幂的计算法则等知识,在解答(3)时要注意进行分类讨论.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
1.一块正方形的瓷砖,面积为$\sqrt{60}$cm2,它的边长大约在( )
| A. | 4cm~5cm之间 | B. | 5cm~6cm之间 | C. | 6cm~7cm之间 | D. | 7cm~8cm之间 |
18. 如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
 如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )| A. | $\frac{AD}{BC}=\frac{CE}{DF}$ | B. | $\frac{AD}{BE}=\frac{BC}{AF}$ | C. | $\frac{AB}{CD}=\frac{CD}{EF}$ | D. | $\frac{AD}{BC}=\frac{DF}{CE}$ |
20.已知2x=3y(xy≠0),则下列各式中错误的是( )
| A. | $\frac{x+y}{y}$=$\frac{5}{2}$ | B. | $\frac{x}{y}$=$\frac{2}{3}$ | C. | $\frac{x-y}{x+y}$=$\frac{1}{5}$ | D. | y=$\frac{2}{3}$x |
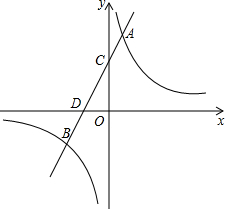 如图,直线y=mx+4与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A、B,与x轴、y轴分别交于D、C,tan∠CDO=2,AC:CD=1:2.
如图,直线y=mx+4与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A、B,与x轴、y轴分别交于D、C,tan∠CDO=2,AC:CD=1:2.