题目内容
7.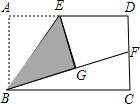 (1)操作发现:如图,小明在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(1)操作发现:如图,小明在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.(2)问题解决:保持(1)中条件不变,若DC=2FC,求$\frac{AD}{AB}$的值.
分析 (1)连接EF,则AE=EG,HL可证明Rt△EGF≌Rt△EDF,根据全等三角形的性质即可求解;
(2)设FC=x,BC=y,则有GF=x,AD=y.根据DC=2FC得到DF=x,DC=AB=BG=2x,BF=BG+GF=3x,然后利用勾股定理得到y与x之间关系,从而求得两条线段的比.
解答 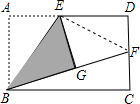 解:(1)同意.连接EF,则∠EGF=∠D=90°.
解:(1)同意.连接EF,则∠EGF=∠D=90°.
∵点E是AD的中点,
∴由折叠的性质知,EG=ED
在Rt△EGF和Rt△EDF中,
$\left\{\begin{array}{l}{EG=ED}\\{EF=EF}\end{array}\right.$,
∴Rt△EGF≌Rt△EDF(HL).
∴GF=DF;
(2)由(1)知,GF=DF.设FC=x,BC=y,则有GF=x,AD=y.
∵DC=2FC,
∴DF=x,DC=AB=BG=2x,
∴BF=BG+GF=3x.
在Rt△BCF中,由勾股定理得:BC2+CF2=BF2,即y2+x2=(3x)2.
∴y=2$\sqrt{2}$x
∴$\frac{AD}{AB}$=$\frac{y}{2x}$=$\sqrt{2}$.
点评 此题考查了矩形的性质、图形的折叠变换、全等三角形的判定和性质、勾股定理的应用等重要知识,难度适中.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
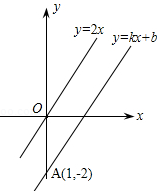 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,-2).
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,-2).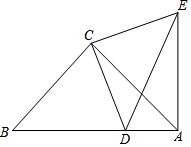 如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB上一点.
如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB上一点.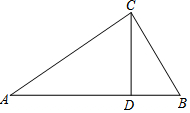 已知:如图,在△ABC中,CD⊥AB,∠B=2∠A.求证:AD=BD+BC.
已知:如图,在△ABC中,CD⊥AB,∠B=2∠A.求证:AD=BD+BC.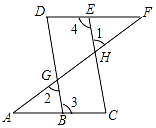 如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F 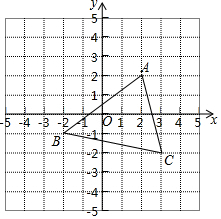 如图,每个小正方形的边长为1个单位
如图,每个小正方形的边长为1个单位