题目内容
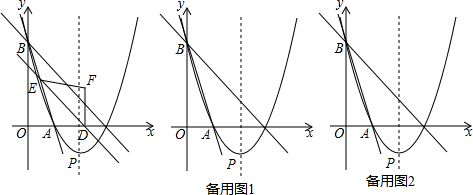
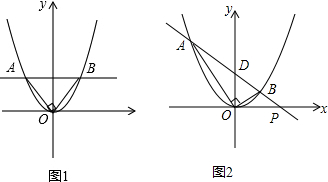
9.在平面直角坐标系中,已知A、B是抛物线y=ax2(a>0)上两个不同的点,其中A在第二象限,B在第一象限.(1)如图1所示,当直线AB与x轴平行,∠AOB=90°,且AB=2时,求此抛物线的解析式和A、B两点的横坐标的乘积;
(2)如图2所示,在(1)所求得的抛物线上,当直线AB与x轴不平行,∠AOB仍为90°时,求证:A、B两点横坐标的乘积是一个定值;
(3)在(2)的条件下,如果直线AB与x轴、y轴分别交于点P、D,且点B的横坐标为$\frac{1}{2}$.那么在x轴上是否存在一点Q,使△QDP为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
分析 (1)由△AOB是等腰直角三角形,求出BE=OE=$\frac{1}{2}$AB=1即可;
(2)先判断出△AMO∽△ONB,然后得到AM×BN=OM×ON,设出点A,B的坐标代换即可;
(3)设出点Q的坐标,分三种情况解方程即可.
解答 解:(1)如图1,
作BE⊥x轴,
∴△AOB是等腰直角三角形,
∴BE=OE=$\frac{1}{2}$AB=1,
∴A(-1,1),B(1,1),
∴A,B两点的横坐标的乘积为-1×1=-1,
∵抛物线y=ax2(a>0)过A,B,
∴a=1,
∴抛物线y=x2,
(2)如图2,
作BN⊥x轴,作AM⊥x轴,
∴∠AOB=AMO=∠BNO=90°,
∴∠MAO=∠BON,
∴△AMO∽△ONB,
∴$\frac{AM}{ON}=\frac{OM}{BN}$,
∴AM×BN=OM×ON,
设A(x1,y1),B(x2,y2)在抛物线上,
∴AM=y1=x12,BN=y2=x22,OM=-x1,ON=x2,
∴x12×x22=-x1×x2,
∴x1×x2=-1,
∴A,B两点横坐标的乘积是一个定值;
(3)由(2)得,A,B两点横坐标的乘积是一个定值为-1,
∵点B的横坐标为$\frac{1}{2}$,
∴点A的横坐标为-2,
∵A,B在抛物线上,
∴A(-2,4),B($\frac{1}{2}$,$\frac{1}{4}$),
∴直线AB解析式为y=-$\frac{3}{2}$x+1,
∴P($\frac{2}{3}$,0),D(0,1)
设Q(n,0),
∴DP2=$\frac{13}{9}$,PQ2=(n-$\frac{2}{3}$)2,DQ2=n2+1
∵△QDP为等腰三角形,
∴①DP=PQ,
∴DP2=PQ2,
∴$\frac{13}{9}$=(n-$\frac{2}{3}$)2,
∴n=$\frac{2±\sqrt{13}}{3}$,
∴Q1($\frac{2+\sqrt{13}}{3}$,0),Q2($\frac{2-\sqrt{13}}{3}$,0)
②DP=DQ,
∴DP2=DQ2,
∴$\frac{13}{9}$=n2+1,
∴n=$\frac{2}{3}$(舍)或n=-$\frac{2}{3}$,
Q3(-$\frac{2}{3}$,0)
③PQ=DQ,
∴PQ2=DQ2,
∴(n-$\frac{2}{3}$)2=n2+1
∴n=-$\frac{5}{12}$,
∴Q4(-$\frac{5}{12}$,0),
∴存在点Q坐标为Q1($\frac{2+\sqrt{13}}{3}$,0),Q2($\frac{2-\sqrt{13}}{3}$,0),Q3(-$\frac{2}{3}$,0),Q4(-$\frac{5}{12}$,0),
点评 此题是二次函数综合题,主要考查了二次函数与一次函数的图象与性质、等腰直角三角形的性质,勾股定理、相似三角形的判定和性质,解本题的关键是用相似三角形的性质得到等积式.

 阅读快车系列答案
阅读快车系列答案| A. | x≥1且x≠2 | B. | x≥2且x≠1 | C. | x≥2 | D. | 都不正确 |
| A. | (x3)2=x5 | B. | x3•x2=x5 | C. | (2x)2=2x2 | D. | (x+2)2=x2+2 |
| A. | a8÷a4=a2 | B. | a3•a4=a12 | C. | $\sqrt{4}$=±2 | D. | 2x3•x2=2x5 |
| A. | a2•a3=a6 | B. | (ab)2=a2b2 | C. | (a2)3=a5 | D. | a2+2a2=3a4 |
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法比较 |
| A. | 1<3+$\sqrt{3}$<2 | B. | 2<3+$\sqrt{3}$<3 | C. | 3<3+$\sqrt{3}$<4 | D. | 4<3+$\sqrt{3}$<5 |
 如图,直线l1与直线l2互相垂直,A,B是两个定点.C,D分别是直线l1,l2上的动点.试确定C,D两点的位置,使四边形ACDB的周长最短.
如图,直线l1与直线l2互相垂直,A,B是两个定点.C,D分别是直线l1,l2上的动点.试确定C,D两点的位置,使四边形ACDB的周长最短.