题目内容
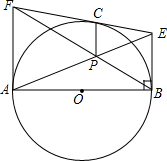如图，AB是⊙O的直径，C是圆上一点，过C点的切线与过A、B两点的切线分别交于E、F两点，AP、BE相交于点P，求证：CP∥AE．考点：切线的性质
专题：证明题
分析：根据切线的性质，由AE和BF为⊙O的切线得到AE⊥AB，BF⊥AB，则AE∥BF，再根据平行线分线段成比例定理得到
=
，接着根据切线长定理得到AE=CE，BF=CF，所以
=
，然后根据平行线分线段成比例定理的逆定理可得CP∥AE．
| AE |
| BF |
| AP |
| FP |
| EC |
| CF |
| AP |
| FP |
解答：证明：∵AE和BF为⊙O的切线，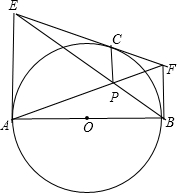
∴AE⊥AB，BF⊥AB，
∴AE∥BF，
∴
=
，
∵EF与⊙O相切于C，
∴AE=CE，BF=CF，
∴
=
，
∴CP∥AE．
∴AE⊥AB，BF⊥AB，
∴AE∥BF，
∴
| AE |
| BF |
| AP |
| FP |
∵EF与⊙O相切于C，
∴AE=CE，BF=CF，
∴
| EC |
| CF |
| AP |
| FP |
∴CP∥AE．
点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了平行线分线段成比例定理．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
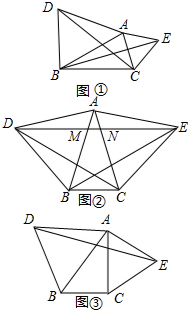（1）如图①，在△ABC中，分别以AB，AC为边作等边△ABD和等边△ACE，猜想CD与BE有什么样的数量关系，直接写出结论，不需证明；
如图，已知，AD为ABC的角平分线，CE⊥AD于点O，CE交AB于E，EF∥BC，求证：∠DEC=∠FEC．
如图，△ADC内接于⊙O，且∠EAC=∠D，求证；AE是⊙O的切线．在平面直角坐标系中，已知A（-1，-1）、B（2，3），若要在x轴上找一点P，使AP+BP最短，则点P的坐标为（ ）
| A、（0，0） | ||
B、（-
| ||
| C、（-1，0） | ||
D、（-
|