题目内容
 如图,已知,AD为ABC的角平分线,CE⊥AD于点O,CE交AB于E,EF∥BC,求证:∠DEC=∠FEC.
如图,已知,AD为ABC的角平分线,CE⊥AD于点O,CE交AB于E,EF∥BC,求证:∠DEC=∠FEC.考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:证明题
分析:根据ASA推出△EOA≌△COA,推出EO=CO,根据线段垂直平分线性质求出DE=DC,根据等腰三角形性质推出∠DEC=∠DCE,根据平行线的性质得出∠FEC=∠DCE即可.
解答:证明:∵CE⊥AD,
∴∠EOA=∠COA=90°,
∵AD平分∠BAC,
∴∠EAD=∠CAD,
在△EOA和△COA中,
,
∴△EOA≌△COA(ASA),
∴EO=CO,
∵CE⊥AD,
∴DE=DC,
∴∠DEC=∠DCE,
∵EF∥BC,
∴∠FEC=∠DCE,
∴∠DEC=∠FEC.
∴∠EOA=∠COA=90°,
∵AD平分∠BAC,
∴∠EAD=∠CAD,
在△EOA和△COA中,
|
∴△EOA≌△COA(ASA),
∴EO=CO,
∵CE⊥AD,
∴DE=DC,
∴∠DEC=∠DCE,
∵EF∥BC,
∴∠FEC=∠DCE,
∴∠DEC=∠FEC.
点评:本题考查了线段垂直平分线性质,等腰三角形的性质,全等三角形的性质和判定,平行线的性质的应用,解此题的关键是求出∠DEC=∠DCE,难度适中.

练习册系列答案
相关题目
 如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是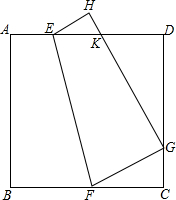 已知:正方形ABCD沿EF折叠,A与H,B与G分别重合,求证:AK+CG=GK.
已知:正方形ABCD沿EF折叠,A与H,B与G分别重合,求证:AK+CG=GK.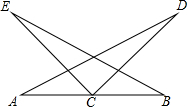 如图,有下列六个论断:①AC=CB,②∠A=∠B,③∠ACE=∠BCD,④CE=CD⑤∠E=∠D,⑥BE=AD.请以其中三个论断作为条件,编拟一个由三个条件能推出一个结论成立的真命题,并证明.
如图,有下列六个论断:①AC=CB,②∠A=∠B,③∠ACE=∠BCD,④CE=CD⑤∠E=∠D,⑥BE=AD.请以其中三个论断作为条件,编拟一个由三个条件能推出一个结论成立的真命题,并证明. 如图,以△ABC的三边为边分别作等边三角形△ADB、△BCF、△ACE.求证:DF=AE.
如图,以△ABC的三边为边分别作等边三角形△ADB、△BCF、△ACE.求证:DF=AE.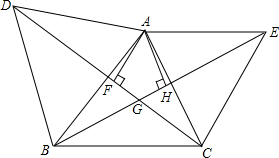 如图,已知△ABD、△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H.
如图,已知△ABD、△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H.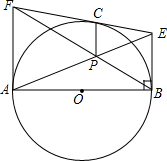 如图,AB是⊙O的直径,C是圆上一点,过C点的切线与过A、B两点的切线分别交于E、F两点,AP、BE相交于点P,求证:CP∥AE.
如图,AB是⊙O的直径,C是圆上一点,过C点的切线与过A、B两点的切线分别交于E、F两点,AP、BE相交于点P,求证:CP∥AE. 画出△ABC关于点A成中心对称的图形.
画出△ABC关于点A成中心对称的图形.