题目内容
台风“菲特”救灾中,某粮食局为保证库存粮食的安全,决定将甲乙两个仓库的粮食,安全转移到具有较强抗台风功能的A,B两个仓库,已知甲库有粮食100吨,乙库有粮食40吨,而A库的容量为80吨,B库的容量为60吨,从甲、乙两库到A、B两库每吨粮食运费如表(单位:元).设甲库运往A库的粮食为x吨.
(1)填表,用x的代数式表示甲乙两库粮食运往到A,B两库粮食吨数.
(2)用x的代数式来表示总运费(元);
(3)若总运费为31200元,则甲库运往A库的粮食应为多少吨?
(4)当x= 时,总运费最省?最省运费是 元(直接写出答案)
| 起点/终点 | A库 | B库 |
| 甲库 | 240 | 250 |
| 乙库 | 180 | 160 |
| 起点/终点 | A库80吨 | B库60吨 |
| 甲库100吨 | x | |
| 乙库40吨 |
(3)若总运费为31200元,则甲库运往A库的粮食应为多少吨?
(4)当x=
考点:一次函数的应用
专题:
分析:(1)根据甲和乙运出的数量正好是A和B缺少的数量,据此即可求解;
(2)根据从甲到A和B以及从乙到A和B的费用的和是31200元,即可列方程求解;
(3)设运费是y,求得x的范围,根据一次函数的性质即可求解.
(2)根据从甲到A和B以及从乙到A和B的费用的和是31200元,即可列方程求解;
(3)设运费是y,求得x的范围,根据一次函数的性质即可求解.
解答:解:(1)甲库向A库运x吨,则剩余的都运到B库,是(100-x)吨,A库中除甲运到的x吨,其余的应该由乙库运,应该是(80-x)吨,
乙库剩余的就是运到B库的吨数40-(80-x)=x-40;
(2)根据题意得:240x+250(100-x)+180(80-x)+160(x-40)=31200,
解得:x=60,
则甲库运往A的粮食是60吨;
(3)设运费是y,则y=240x+250(100-x)+180(80-x)+160(x-40),即y=-30x+33000,
∵40≤x≤80,
则当x=80时,总运费最省,最省运费是:-30×80+33000=30600(元).
故答案是:80,30600.
乙库剩余的就是运到B库的吨数40-(80-x)=x-40;
(2)根据题意得:240x+250(100-x)+180(80-x)+160(x-40)=31200,
解得:x=60,
则甲库运往A的粮食是60吨;
(3)设运费是y,则y=240x+250(100-x)+180(80-x)+160(x-40),即y=-30x+33000,
∵40≤x≤80,
则当x=80时,总运费最省,最省运费是:-30×80+33000=30600(元).
故答案是:80,30600.
点评:本题考查了一次函数的应用,正确理清从甲到A和B以及从乙到A和B的数量是关键.

练习册系列答案
相关题目
y=x+2的图象大致是( )
A、 |
B、 |
C、 |
D、 |
 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )| A、c>-1 |
| B、9a+c>3b |
| C、2a+b≠0 |
| D、b>0 |
 如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是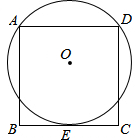 如图,正方形ABCD的边BC与⊙O相切于点E,点A、D在⊙O上.若AB=10,则⊙O的半径是
如图,正方形ABCD的边BC与⊙O相切于点E,点A、D在⊙O上.若AB=10,则⊙O的半径是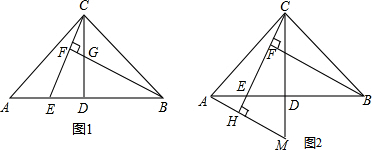
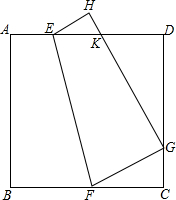 已知:正方形ABCD沿EF折叠,A与H,B与G分别重合,求证:AK+CG=GK.
已知:正方形ABCD沿EF折叠,A与H,B与G分别重合,求证:AK+CG=GK.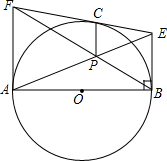 如图,AB是⊙O的直径,C是圆上一点,过C点的切线与过A、B两点的切线分别交于E、F两点,AP、BE相交于点P,求证:CP∥AE.
如图,AB是⊙O的直径,C是圆上一点,过C点的切线与过A、B两点的切线分别交于E、F两点,AP、BE相交于点P,求证:CP∥AE.