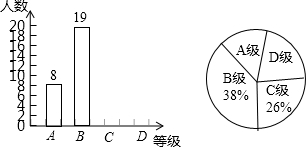
题目内容
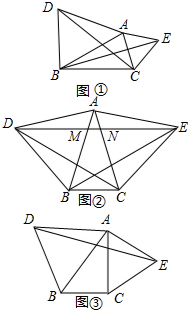 (1)如图①,在△ABC中,分别以AB,AC为边作等边△ABD和等边△ACE,猜想CD与BE有什么样的数量关系,直接写出结论,不需证明;
(1)如图①,在△ABC中,分别以AB,AC为边作等边△ABD和等边△ACE,猜想CD与BE有什么样的数量关系,直接写出结论,不需证明;(2)如图②,在(1)的条件下,若△ABC中,AB=AC,连结DE分别交AB、AC于点M、N,猜想DM与EN有什么样的数量关系,证明你的结论;
(3)如图③,在(1)的条件下,若△ABC中,∠ACB=90°,∠BAC=30°,连结DE分别交AB、AC于点M、N,则有DM=EM,请证明.
考点:全等三角形的判定与性质
专题:
分析:(1)根据等边三角形性质得出AD=AB,AC=AE,∠DAB=∠EAC=60°,求出∠DAC=∠BAE,根据SAS推出△DAC≌△BAE即可;
(2)根据等边三角形的性质得出AD=AB,AC=AE,∠DAB=∠EAC=60°,求出AD=AE,AM=AN,根据SAS推出△ADM≌△AEN即可;
(3)过D作DG⊥AB于G,证△DGB≌△ACB,推出DG=AC,求出AE=DG,∠EAM=∠DGA,根据AAS推出△DGM≌△EAM即可.
(2)根据等边三角形的性质得出AD=AB,AC=AE,∠DAB=∠EAC=60°,求出AD=AE,AM=AN,根据SAS推出△ADM≌△AEN即可;
(3)过D作DG⊥AB于G,证△DGB≌△ACB,推出DG=AC,求出AE=DG,∠EAM=∠DGA,根据AAS推出△DGM≌△EAM即可.
解答:解:(1)CD=EB,
理由是:∵△ABD和△ACE是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴CD=EB;
(2)DM=EN,
证明:∵△ABD和△ACE是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠EAC=60°,
∵AB=AC,
∴AD=AE,
∴∠ADE=∠AED,
∴∠AMN=∠ADE+∠EAB,∠ANM=∠AED+∠EAC,
∴∠AMN=∠ANM,
∴AM=AN,
在△ADM和△AEN中,
,
∴△ADM≌△AEN(SAS),
∵DM=EN;
(3)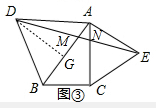 证明:过D作DG⊥AB于G,
证明:过D作DG⊥AB于G,
则∠DGB=∠ACB=90°,
在△DGB和△ACB中,
,
∴△DGB≌△ACB(AAS),
∴DG=AC,
∵AE=AC,
∴AE=DG,
∵∠EAM=60°+30°=90°=∠DGA,
在△DGM和△EAM中,
,
∴△DGM≌△EAM(AAS),
∴DM=EM.
理由是:∵△ABD和△ACE是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
|
∴△DAC≌△BAE(SAS),
∴CD=EB;
(2)DM=EN,
证明:∵△ABD和△ACE是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠EAC=60°,
∵AB=AC,
∴AD=AE,
∴∠ADE=∠AED,
∴∠AMN=∠ADE+∠EAB,∠ANM=∠AED+∠EAC,
∴∠AMN=∠ANM,
∴AM=AN,
在△ADM和△AEN中,
|
∴△ADM≌△AEN(SAS),
∵DM=EN;
(3)
 证明:过D作DG⊥AB于G,
证明:过D作DG⊥AB于G,则∠DGB=∠ACB=90°,
在△DGB和△ACB中,
|
∴△DGB≌△ACB(AAS),
∴DG=AC,
∵AE=AC,
∴AE=DG,
∵∠EAM=60°+30°=90°=∠DGA,
在△DGM和△EAM中,
|
∴△DGM≌△EAM(AAS),
∴DM=EM.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质的应用,全等三角形的判定结合全等三角形的性质证明线段相等或角相等的工具,注意:全等三角形的对应边相等,对应角相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
y=x+2的图象大致是( )
A、 |
B、 |
C、 |
D、 |
 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )| A、c>-1 |
| B、9a+c>3b |
| C、2a+b≠0 |
| D、b>0 |
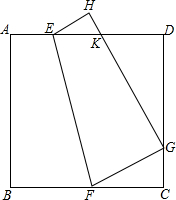 已知:正方形ABCD沿EF折叠,A与H,B与G分别重合,求证:AK+CG=GK.
已知:正方形ABCD沿EF折叠,A与H,B与G分别重合,求证:AK+CG=GK.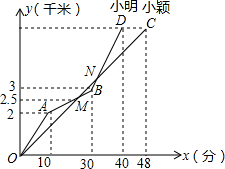 小明、小颖两名同学在学校冬季越野赛中的路程y(千米)与时间x(分)的函数关系如图所示.
小明、小颖两名同学在学校冬季越野赛中的路程y(千米)与时间x(分)的函数关系如图所示.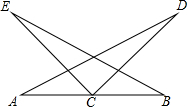 如图,有下列六个论断:①AC=CB,②∠A=∠B,③∠ACE=∠BCD,④CE=CD⑤∠E=∠D,⑥BE=AD.请以其中三个论断作为条件,编拟一个由三个条件能推出一个结论成立的真命题,并证明.
如图,有下列六个论断:①AC=CB,②∠A=∠B,③∠ACE=∠BCD,④CE=CD⑤∠E=∠D,⑥BE=AD.请以其中三个论断作为条件,编拟一个由三个条件能推出一个结论成立的真命题,并证明. 如图,以△ABC的三边为边分别作等边三角形△ADB、△BCF、△ACE.求证:DF=AE.
如图,以△ABC的三边为边分别作等边三角形△ADB、△BCF、△ACE.求证:DF=AE.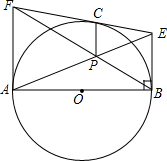 如图,AB是⊙O的直径,C是圆上一点,过C点的切线与过A、B两点的切线分别交于E、F两点,AP、BE相交于点P,求证:CP∥AE.
如图,AB是⊙O的直径,C是圆上一点,过C点的切线与过A、B两点的切线分别交于E、F两点,AP、BE相交于点P,求证:CP∥AE.