题目内容
5.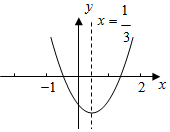 如图所示的二次函数 y=ax2+bx+c 的图象中,观察得出了下面五条信息:
如图所示的二次函数 y=ax2+bx+c 的图象中,观察得出了下面五条信息:①c<0;②abc>0;
③a+b+c>0;④2a-3b=0;
⑤c-4b>0.
其中正确信息是( )
| A. | ①②③ | B. | ①②④ | C. | ①②⑤ | D. | ①②③④ |
分析 根据函数图象可得各系数的关系:a>0,b<0,c<0,再结合图象判断各结论.
解答 解:由函数图象可得各系数的关系:a>0,b<0,c<0,
则①c<0,正确;
②abc>0,正确;
③当x=1,a+b+c<0,错误;
④对称轴x=-$\frac{b}{2a}$=$\frac{1}{3}$,2a+3b=0,错误;
⑤由于a-b+c>0,则c-$\frac{5}{2}$b>0,
又-$\frac{3}{2}$b>0,c-4b>0,正确.
故正确的结论有①②⑤,
故选:C.
点评 本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.

练习册系列答案
相关题目
16.下列变形中正确的是( )
| A. | 由3x=4x+1得4x-3x=1 | B. | 由2(3-x)=5得6-x=5 | ||
| C. | 由-4x<3得$x>-\frac{3}{4}$ | D. | 由3x>-2得$x<-\frac{2}{3}$ |
13.已知sinB=$\frac{\sqrt{2}}{2}$,则∠B等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
20.抛物线 y=(x-1)2-2 的顶点是( )
| A. | (1,-2) | B. | (-1,2) | C. | (1,2) | D. | (-1,-2) |
10.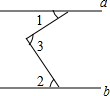 如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
 如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
如图,己知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )| A. | 100° | B. | 90° | C. | 70° | D. | 50° |
17.若(a2+b2-5)2=25,则a2+b2=( )
| A. | 8或-2 | B. | -2 | C. | 8 | D. | 0或10 |
