题目内容
如图梯形ABCD中，AD∥BC，梯形ABCD上底的有任意一点M，连结BM，过A和M分别作BM、AB的平行线交于点E．求证：DE=DC．
考点：平行线分线段成比例,平行四边形的判定与性质
专题：
分析：连结BE交AM于点O．由题意易证四边形ABME是平行四边形，所以OE=OB；有AD∥BC可以得出
=
，故DE=DC．
| ED |
| DC |
| OE |
| OB |
解答：
解：如图，∵AE∥BM，AB∥EM，
∴四边形ABME是平行四边形，
∴OE=OB．
又∵AD∥BC，
∴
=
，
∴DE=DC．
解：如图，∵AE∥BM，AB∥EM，∴四边形ABME是平行四边形，
∴OE=OB．
又∵AD∥BC，
∴
| ED |
| DC |
| OE |
| OB |
∴DE=DC．
点评：本题考查了平行线分线段成比例、平行四边形的判定与性质．凡是可以用平行四边形知识证明的问题，不要再回到用三角形全等证明，应直接运用平行四边形的性质和判定去解决问题．
练习册系列答案
相关题目
如图，平面直角坐标系中，点A的坐标（6，0），点P在直线y=-2x+m上，且AP=OP=5，求m的值．
如图，P是正方形ABCD对角线BD上一点，PE⊥DC，PF⊥BC，垂足分别为点E、F．请判断AP与EF的数量关系，并证明你的判断．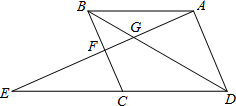
如图，点E为平行四边形ABCD中DC延长线上的一点，且CE=DC．连结AE，分别交BC、BD于点F、G．若BD=6，求DG的长．