题目内容
11.(1)已知AB、CD是圆O的两条相交弦,交点为P,证明:PC•PD=PA•PB;(2)已知PAB、PCD是圆O的两条割线,PT是圆的切线,证明:PT2=PC•PD=PA•PB.
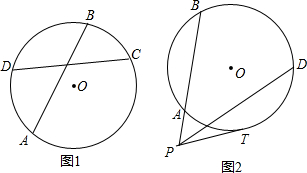
分析 (1)连接AC、DB,根据同弧所对的圆周角相等,证出△ACP∽△DBP,然后根据相似三角形的性质得出结论;
(2)连接AT,BT,根据弦切角定理证得∠B=∠ATP,推出△BPT∽△TPA,然后根据相似三角形的性质得出结论.
解答 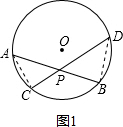 证明:(1)如图1,连接AC、BD.
证明:(1)如图1,连接AC、BD.
∵∠A=∠D,∠C=∠B,
∴△ACP∽△DBP,
∴$\frac{PA}{PD}$=$\frac{PC}{PB}$,
∴PA•PB=PC•PD;
(2)如图2,连接AT,BT,
∵PT是圆的切线,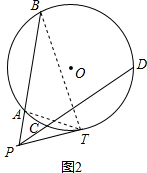
∴∠B=∠ATP,
∵∠APT=∠BPT,
∴△BPT∽△TPA,
∴$\frac{PB}{PT}=\frac{PT}{PA}$,
∴PT2=PA•PB,
同理PT2=PC•PD,
∴PT2=PC•PD=PA•PB.
点评 本题主要考查了圆周角的性质定理,弦切角定理,相似三角形的判定和性质,通过相似三角形的性质来证明相交弦定理,和切割线定理,关键是根据圆周角定理弦切角定理求出相等的角.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
1. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′位置,且CC′∥AB,则∠CAB′的度数是( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′位置,且CC′∥AB,则∠CAB′的度数是( )
 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′位置,且CC′∥AB,则∠CAB′的度数是( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′位置,且CC′∥AB,则∠CAB′的度数是( )| A. | 30° | B. | 45° | C. | 40° | D. | 50° |
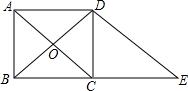 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点D作DE∥AC,交BC的延长线于点E.求证:BD=DE.
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点D作DE∥AC,交BC的延长线于点E.求证:BD=DE.