题目内容
16.是否存在a,b使$\frac{1}{a}$+$\frac{1}{b}$-$\frac{1}{a+b}$=0成立.分析 已知等式整理,把b看做已知数求出a,得到a无解,故不存在.
解答 解:已知等式整理得:$\frac{a+b}{ab}$=$\frac{1}{a+b}$,即(a+b)2=ab,
即a2+b2+ab=0,
解得:a=$\frac{-b±\sqrt{{b}^{2}-4{b}^{2}}}{2}$=$\frac{-b±\sqrt{-3{b}^{2}}}{2}$,即a无解,
则不存在a,b使$\frac{1}{a}$+$\frac{1}{b}$-$\frac{1}{a+b}$=0成立.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
6.今年马铃薯喜获丰收,某生产基地收获马铃薯40吨.经市场调查,可采用批发、零售、加工销售三种销售方式,这三种销售方式每吨马铃薯的利润如表:
设按计划全部销售出后的总利润为y元,其中排放量为x吨,且加工销售量为15吨.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完马铃薯后获得的最大利润.
| 销售方式 | 批发 | 零售 | 加工销售 |
| 利润(元/吨) | 1200 | 2200 | 3000 |
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完马铃薯后获得的最大利润.
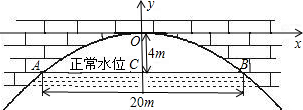 如图,有一抛物线形拱桥,正常水位时桥下水面宽20m,拱顶距离水面4m.已知其抛物线解析式为y=-0.04x2,在正常水位时,桥下的水深为2m,为保证过往船只顺利通行,桥下水面的宽度不得小于18m,求水深超过多少米时,就会影响过往船只从桥下顺利通行?
如图,有一抛物线形拱桥,正常水位时桥下水面宽20m,拱顶距离水面4m.已知其抛物线解析式为y=-0.04x2,在正常水位时,桥下的水深为2m,为保证过往船只顺利通行,桥下水面的宽度不得小于18m,求水深超过多少米时,就会影响过往船只从桥下顺利通行?