题目内容
6.解方程:x2-2x-2$\sqrt{2}$x+3+2$\sqrt{2}$=0.分析 方程整理后,利用完全平方公式变形,开方即可求出解.
解答 解:方程整理得:x2-(2+2$\sqrt{2}$)x=-3-2$\sqrt{2}$,
配方得:x2-(2+2$\sqrt{2}$)x+3+2$\sqrt{2}$=0,即(x-1-$\sqrt{2}$)2=0,
开方得:x1=x2=1+$\sqrt{2}$.
点评 此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.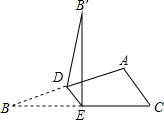 如图,在△ABC中,点D、E分别是AB、BC边的中点,∠B=23°,∠C=40°,将△ABC沿DE折叠,点B的对应点是B′,则∠ADB′的度数是( )
如图,在△ABC中,点D、E分别是AB、BC边的中点,∠B=23°,∠C=40°,将△ABC沿DE折叠,点B的对应点是B′,则∠ADB′的度数是( )
 如图,在△ABC中,点D、E分别是AB、BC边的中点,∠B=23°,∠C=40°,将△ABC沿DE折叠,点B的对应点是B′,则∠ADB′的度数是( )
如图,在△ABC中,点D、E分别是AB、BC边的中点,∠B=23°,∠C=40°,将△ABC沿DE折叠,点B的对应点是B′,则∠ADB′的度数是( )| A. | 45° | B. | 54° | C. | 60° | D. | 65° |
16.已知P(-3,-4),则P点到y轴的距离为( )
| A. | 5 | B. | 4 | C. | 3.5 | D. | 3 |
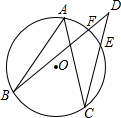 如图,点A,B,C在⊙O上,点D在圆外,∠ABD=15°,CD,BD分别交⊙O于点E,F,且F是$\widehat{AE}$的中点,∠D=35°,求∠BAC的度数.
如图,点A,B,C在⊙O上,点D在圆外,∠ABD=15°,CD,BD分别交⊙O于点E,F,且F是$\widehat{AE}$的中点,∠D=35°,求∠BAC的度数.