题目内容
19. 如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )
如图,等腰梯形ABCD中,AD∥BC,AC,BD交于点O,下列结论错误的是( )| A. | △ABO≌△DCO | B. | AO=DO | C. | AC=DB | D. | BD平分∠ABC |
分析 先由SAS证明△ABD≌△DCA,得出∠ABO=∠DCO,AC=BD,再由AAS证明△ABO≌△DCO,得出AO=DO,即可得出结论.
解答 解:∵等腰梯形ABCD中,AD∥BC,
∴AB=DC,∠BAD=∠CDA,
在△ABD和△DCA中,$\left\{\begin{array}{l}{AB=DC}&{\;}\\{∠BAD=∠CDA}&{\;}\\{AD=AD}&{\;}\end{array}\right.$,
∴△ABD≌△DCA(SAS),
∴∠ABO=∠DCO,AC=BD,
在△ABO和△DCO中,
$\left\{\begin{array}{l}{∠ABO=∠DCO}&{\;}\\{∠AOB=∠DOC}&{\;}\\{AB=DC}&{\;}\end{array}\right.$,
∴△ABO≌△DCO(AAS),
∴AO=DO,
即①②③正确,④错误;
故选:D.
点评 本题考查了等腰梯形的性质、全等三角形的判定与性质;熟练掌握等腰梯形的性质得出相等的边和角证明三角形全等是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
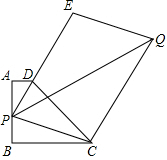 已知梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,以PE、PC为边作?PCQE,则对角线PQ的最小值为7.
已知梯形ABCD中,AD∥BC,∠B=90°,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,以PE、PC为边作?PCQE,则对角线PQ的最小值为7. 如图,D为圆O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
如图,D为圆O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. 如图,在△ABC中,DE∥BC,EC=2AE,BD=6,则AD=3.
如图,在△ABC中,DE∥BC,EC=2AE,BD=6,则AD=3. 某校八年级共四个班,各班寒假外出旅游的学生人数如图所示,那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为40%.
某校八年级共四个班,各班寒假外出旅游的学生人数如图所示,那么三班外出旅游学生人数占全年级外出旅游学生人数的百分比为40%.