题目内容
(1)计算:(-1)0+2sin30°+(
)2;
(2)解不等式组:
,并将它的解集在数轴上表示出来.
| 3 |
(2)解不等式组:
|

考点:解一元一次不等式组,实数的运算,零指数幂,在数轴上表示不等式的解集,特殊角的三角函数值
专题:计算题,压轴题
分析:(1)分别根据0指数幂、特殊角度的三角函数值计算出各数,再根据有理数混合运算的法则进行计算;
(2)分别求出各不等式的解集,再求出其公共解集,在数轴上表示出来即可.
(2)分别求出各不等式的解集,再求出其公共解集,在数轴上表示出来即可.
解答:解:(1)原式=1+1+3
=5;
(2)解:
,
由①得x≥-4,
由②得x<-1,
不等式组的解:-4≤x<-1,
在数轴上表示为:

=5;
(2)解:
|
由①得x≥-4,
由②得x<-1,
不等式组的解:-4≤x<-1,
在数轴上表示为:

点评:本题考查的是有理数的混合运算及解一元一次不等式组、在数轴上表示不等式组的解集等知识,熟知实心圆点与空心圆点的区别是解答此题的关键.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
由四名同学每人书写一个不同的实系数一元二次方程,他们所提供的四个方程中恰好有两个方程没有实数根的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若有理数a,b在数轴上的位置如图所示,则下列各式中正确的是( )


| A、-a>b | ||||
B、
| ||||
| C、a+b>1 | ||||
D、-
|
若a、b为非零实数,下列说法正确的是( )
A、a2-ab+
| ||||
| B、|a+b|≥|a-b| | ||||
C、若a>b,则
| ||||
D、(a+1)x>b的解集为x>
|
将平面直角坐标系的某点的坐标向上或向下平移,则( )
| A、横坐标不变 |
| B、纵坐标不变 |
| C、横、纵坐标都变 |
| D、无法确定 |
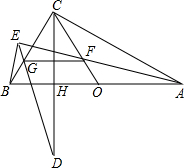 如图,O是Rt△ABC斜边AB的中点,CH⊥AB于H,延长CH至D,使得CH=DH,F为CO上任意一点,过B作BE⊥AF于E,连接DE交BC于G.
如图,O是Rt△ABC斜边AB的中点,CH⊥AB于H,延长CH至D,使得CH=DH,F为CO上任意一点,过B作BE⊥AF于E,连接DE交BC于G. 如图,在平面直角坐标系中,点P(3,4),以点P为圆心的⊙P与两坐标轴共有3个交点,则⊙P的半径r的取值为
如图,在平面直角坐标系中,点P(3,4),以点P为圆心的⊙P与两坐标轴共有3个交点,则⊙P的半径r的取值为