题目内容
如图,将一个边长为1的正方形纸片ABCD折叠,使点B落在边AD上 不与A、D重合.MN为折痕,折叠后B′C′与DN交于P.
Ⅰ连接B B′,那么B B′与MN的长度相等吗?为什么?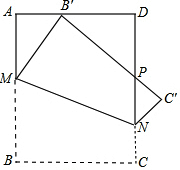
Ⅱ设BM=y,AB′=x,求y与x的函数关系式;
Ⅲ猜想当B点落在什么位置上时,折叠起来的梯形MN C′B′面积最小?并验证你的猜想.
Ⅰ连接B B′,那么B B′与MN的长度相等吗?为什么?

Ⅱ设BM=y,AB′=x,求y与x的函数关系式;
Ⅲ猜想当B点落在什么位置上时,折叠起来的梯形MN C′B′面积最小?并验证你的猜想.
考点:翻折变换(折叠问题)
专题:
分析:Ⅰ、根据折叠的性质可知,∠A=∠MRN=90°,又∵∠ABB′=∠RNM,RN=AB=1,可知△ABB′≌△RNM,继而可知BB′=MN;
Ⅱ、由Ⅰ可知△MQB∽△B′AB,根据相似三角形的性质得到求y与x的函数关系式;
Ⅲ、由Ⅱ可得到MB′和CN的表达式,继而根据梯形的面积公式求出S的表达式,利用二次函数求出S的最小值.
Ⅱ、由Ⅰ可知△MQB∽△B′AB,根据相似三角形的性质得到求y与x的函数关系式;
Ⅲ、由Ⅱ可得到MB′和CN的表达式,继而根据梯形的面积公式求出S的表达式,利用二次函数求出S的最小值.
解答:解:Ⅰ、过点N作NR⊥AB,垂足为R,连接BB′交MN于点Q.
 则由折叠知,△MBQ与△MB′Q关于直线MN对称,
则由折叠知,△MBQ与△MB′Q关于直线MN对称,
∴MQ⊥BB′.(4分)
在△RNM和△ABB′中,∠A=∠MRN=90°,(5分)
∠ABB′+∠BMQ=∠RNM+∠BMN=90°
∴∠ABB′=∠RNM,(6分)
又∵RN=AB=1,(7分)
∴△RNM≌△ABB′,
∴BB′=MN.(8分)
Ⅱ、由Ⅰ可知△MQB∽△B′AB,
∵
=
=
,(9分)
∵AB′=x,
则BB′=
,BQ=
,代入上式得:
BM=
(x2+1).(10分)
Ⅲ、由Ⅱ得:BM=
(x2+1),
CN=BR=BM-MR=
(x2+1)-x=
(x-1)2,(11分)
∵MB′∥NC′,
∴四边形MNC′B′是梯形,
∴S=
[
(x-1)2+
(x2+1)]×1=
(x2-x+1),(12分)
由S=
(x2-x+1)=
(x-
)2+
,
故当x=
时,即B落在AD的中点处时,梯形面积最小,其最小值为
.
 则由折叠知,△MBQ与△MB′Q关于直线MN对称,
则由折叠知,△MBQ与△MB′Q关于直线MN对称,∴MQ⊥BB′.(4分)
在△RNM和△ABB′中,∠A=∠MRN=90°,(5分)
∠ABB′+∠BMQ=∠RNM+∠BMN=90°
∴∠ABB′=∠RNM,(6分)
又∵RN=AB=1,(7分)
∴△RNM≌△ABB′,
∴BB′=MN.(8分)
Ⅱ、由Ⅰ可知△MQB∽△B′AB,
∵
| AB′ |
| MQ |
| AB |
| BQ |
| BB′ |
| MB |
∵AB′=x,
则BB′=
| 1+x2 |
| 1 |
| 2 |
| 1+x2 |
BM=
| 1 |
| 2 |
Ⅲ、由Ⅱ得:BM=
| 1 |
| 2 |
CN=BR=BM-MR=
| 1 |
| 2 |
| 1 |
| 2 |
∵MB′∥NC′,
∴四边形MNC′B′是梯形,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
故当x=
| 1 |
| 2 |
| 3 |
| 8 |
点评:此题考查了翻折变换,要注意翻折不变性和正方形的性质等隐含条件.题目还涉及二次函数的最值问题,综合性较强.

练习册系列答案
相关题目
下列运算正确的是( )
| A、(3a)3=9a3 | ||||||||
B、
| ||||||||
C、(x+
| ||||||||
| D、-2100+2101=2 |
下面四句关于约数和倍数的话中正确的是( )
| A、正整数a和b的最小公倍数一定小于ab |
| B、正整数a和b的最大公约数一定不大于a |
| C、正整数a和b的最小公倍数一定不小于ab |
| D、正整数a和b的最大公约数一定大于a |
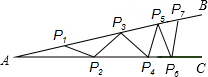 如图,为了加固屋顶的钢架,焊上等长的钢条(P1P2、P2P3等).若∠A=15°,AP1=P1P2,则这样的钢条最多只能焊上( )条.
如图,为了加固屋顶的钢架,焊上等长的钢条(P1P2、P2P3等).若∠A=15°,AP1=P1P2,则这样的钢条最多只能焊上( )条. 如图,将△ABC绕点C旋转60°得到△A′B′C′,已知AC=6,BC=4,则线段AB扫过图形(阴影部分)的面积为
如图,将△ABC绕点C旋转60°得到△A′B′C′,已知AC=6,BC=4,则线段AB扫过图形(阴影部分)的面积为

 若现在需要在电话中告诉你的同学如图的图形,你将怎么说?提供两种.
若现在需要在电话中告诉你的同学如图的图形,你将怎么说?提供两种.