题目内容
由四名同学每人书写一个不同的实系数一元二次方程,他们所提供的四个方程中恰好有两个方程没有实数根的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列表法与树状图法
专题:
分析:根据已知得出假设方程为A,B,C,D,即用A无,A有表示有无实数根,列出树状图进而得出四个方程中恰好有两个方程没有实数根的概率.
解答:解:根据题意可以假设方程为A,B,C,D,即用A无,A有表示有无实数根,
如图所示:

∵他们所提供的四个方程中恰好有两个方程没有实数根的一共有6种,
∴他们所提供的四个方程中恰好有两个方程没有实数根的概率为:
=
.
故选:D.
如图所示:

∵他们所提供的四个方程中恰好有两个方程没有实数根的一共有6种,
∴他们所提供的四个方程中恰好有两个方程没有实数根的概率为:
| 6 |
| 16 |
| 3 |
| 8 |
故选:D.
点评:此题主要考查了树状图法求概率,树状图法适用于两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
已知实数a、b分别满足
-
-3=0和b4+b2-3=0,则代数式
的值等于( )
| 4 |
| a4 |
| 2 |
| a2 |
| a4b4+4 |
| a4 |
| A、175 | B、55 | C、13 | D、7 |
有面额为壹元、贰元、伍元的人民币共10张,欲用来购买一盏价值为18元的护眼灯,要求三种面额都用上,则不同的付款方式有( )
| A、3种 | B、4种 | C、7种 | D、8种 |
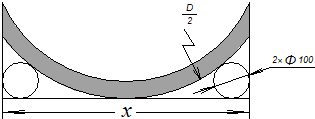 两侧,测量大的圆形工件的直径,设两圆钢棒的外侧的距离为xmm,工件的直径为Dmm.
两侧,测量大的圆形工件的直径,设两圆钢棒的外侧的距离为xmm,工件的直径为Dmm.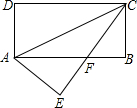 如图,ABCD为矩形,AB=a,BC=b(a>b),以对角线AC为对称轴将△ADC沿AC对折,则D点转移到E处,CE与AB交于F,则△AFC的面积为
如图,ABCD为矩形,AB=a,BC=b(a>b),以对角线AC为对称轴将△ADC沿AC对折,则D点转移到E处,CE与AB交于F,则△AFC的面积为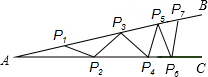 如图,为了加固屋顶的钢架,焊上等长的钢条(P1P2、P2P3等).若∠A=15°,AP1=P1P2,则这样的钢条最多只能焊上( )条.
如图,为了加固屋顶的钢架,焊上等长的钢条(P1P2、P2P3等).若∠A=15°,AP1=P1P2,则这样的钢条最多只能焊上( )条.