题目内容
2014年3月,YC市举办了首届中学生汉字听写大会,从甲、乙、丙、丁4套题中随机抽取一套训练,抽中甲的概率是( )
A. 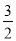 B.
B. 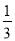 C.
C. 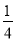 D.
D. 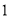
 C
【解析】试题分析:根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率. 因此,
∵从甲、乙、丙、丁4套题中随机抽取一套训练,∴抽中甲的概率是.故选C.
C
【解析】试题分析:根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率. 因此,
∵从甲、乙、丙、丁4套题中随机抽取一套训练,∴抽中甲的概率是.故选C.
练习册系列答案
相关题目
如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=__度.
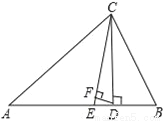
 74°
【解析】试题解析:
∵CE平分∠ACB,CD⊥AB于D,
∵DF⊥CE,
故答案为:74.
74°
【解析】试题解析:
∵CE平分∠ACB,CD⊥AB于D,
∵DF⊥CE,
故答案为:74. 如图,△AOD关于直线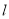 进行轴对称变换后得到△BOC,下列不正确的是().
进行轴对称变换后得到△BOC,下列不正确的是().
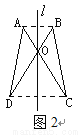
A. ∠DAO=∠CBO,∠ADO=∠BCO B. 直线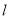 垂直平分AB、CD
垂直平分AB、CD
C. △AO D和△BOC均是等腰三角形 D. AD=BC,OD=OC
 C
【解析】试题分析:根据轴对称图形的性质可得:A、B、D为正确答案;△OAB和△DOC为等腰三角形.
C
【解析】试题分析:根据轴对称图形的性质可得:A、B、D为正确答案;△OAB和△DOC为等腰三角形. 一个不透明的盒子中装有10个黑球和若干个白球,它们除颜色不同外,其余均相同,从盒子中随机摸出一球记下其颜色,再把它放回盒子中摇匀,重复上述过程,共试验400次,其中有240次摸到白球,由此估计盒子中的白球大约有________个.
 15
【解析】试题解析:∵共试验400次,其中有240次摸到白球,
∴白球所占的比例为,
设盒子中共有白球x个,则,
解得:x=15.
15
【解析】试题解析:∵共试验400次,其中有240次摸到白球,
∴白球所占的比例为,
设盒子中共有白球x个,则,
解得:x=15. 如图,在空白网格内将某一个小正方形涂成阴影部分,且所涂的小正方形与原阴影图形的小正方形至少有一边重合.小红按要求涂了一个正方形,所得到的阴影图形恰好是轴对称图形的概率为( )

A. B.
B. C.
C.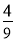 D.
D.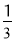
 C.
【解析】
试题分析:如图所示:所涂的小正方形与原阴影图形的小正方形至少有一边重合的一共有9个,
能构成轴对称图形的有所标数据1,2,3,4,共4个,则所得到的阴影图形恰好是轴对称图形的概率为:.
故选:C.
C.
【解析】
试题分析:如图所示:所涂的小正方形与原阴影图形的小正方形至少有一边重合的一共有9个,
能构成轴对称图形的有所标数据1,2,3,4,共4个,则所得到的阴影图形恰好是轴对称图形的概率为:.
故选:C. 如图,已知在△ABC中,AD⊥BC于点D,AE平分∠BAC,判断∠EAD与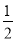 (∠C-∠B)的关系,并说明理由.
(∠C-∠B)的关系,并说明理由.
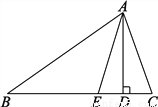
 ∠EAD= (∠C-∠B).理由见解析
【解析】试题分析:根据三角形内角和定理求出求出∠DAC和∠EAC,相减即可得出答案.
试题解析:
理由是:
∵AE平分∠BAC,
∵AD⊥BC,
∠EAD= (∠C-∠B).理由见解析
【解析】试题分析:根据三角形内角和定理求出求出∠DAC和∠EAC,相减即可得出答案.
试题解析:
理由是:
∵AE平分∠BAC,
∵AD⊥BC, 如图所示, AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.
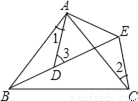
 55°
【解析】求出∠BAD=∠EAC,证△BAD≌△EAC,推出∠2=∠ABD=30°,根据三角形的外角性质求出即可.
【解析】
∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△EAC中,
AB=AC,∠BAD=∠EAC,
∴△BAD≌△EAC(SAS),
∴∠2=∠ABD=30°,
∵...
55°
【解析】求出∠BAD=∠EAC,证△BAD≌△EAC,推出∠2=∠ABD=30°,根据三角形的外角性质求出即可.
【解析】
∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△EAC中,
AB=AC,∠BAD=∠EAC,
∴△BAD≌△EAC(SAS),
∴∠2=∠ABD=30°,
∵... △ABC中,AB = 5,AC = 6,BC = 4,边AB的垂直平分线交AC于点D,则△BDC的周长是( )
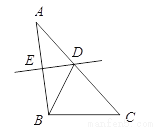
A. 8 B. 9 C. 10 D. 11
 C
【解析】试题分析:由ED是AB的垂直平分线,可得AD=BD,又由△BDC的周长=DB+BC+CD,即可得△BDC的周长=AD+BC+CD=AC+BC. ∵ED是AB的垂直平分线, ∴AD=BD,
∵△BDC的周长=DB+BC+CD, ∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10.
C
【解析】试题分析:由ED是AB的垂直平分线,可得AD=BD,又由△BDC的周长=DB+BC+CD,即可得△BDC的周长=AD+BC+CD=AC+BC. ∵ED是AB的垂直平分线, ∴AD=BD,
∵△BDC的周长=DB+BC+CD, ∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10. 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=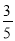 ,则DE=____________.
,则DE=____________.
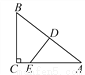
 【解析】试题分析:在Rt△ABC中,先求出AB,AC继而得出AD,再由△ADE∽△ACB,利用对应边成比例可求出DE.
试题解析:∵BC=6,sinA=,
∴AB=10,
∴AC=,
∵D是AB的中点,
∴AD=AB=5,
∵△ADE∽△ACB,
∴,即,
解得:DE=.
考点: 1.解直角三角形;2.线段垂直平分线的性质;3勾股定理.
...
【解析】试题分析:在Rt△ABC中,先求出AB,AC继而得出AD,再由△ADE∽△ACB,利用对应边成比例可求出DE.
试题解析:∵BC=6,sinA=,
∴AB=10,
∴AC=,
∵D是AB的中点,
∴AD=AB=5,
∵△ADE∽△ACB,
∴,即,
解得:DE=.
考点: 1.解直角三角形;2.线段垂直平分线的性质;3勾股定理.
... 
