题目内容
7. 在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{4}{x}$的一个交点为A(m,2),与y轴分别交于点B.
在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{4}{x}$的一个交点为A(m,2),与y轴分别交于点B.(1)求m和b的值;
(2)若点C在y轴上,且△ABC的面积是2,请直接写出点C的坐标.
分析 (1)根据点A(m,2)在双曲线y=$\frac{4}{x}$上可以求得m的值,再将点A的坐标代入y=$\frac{1}{2}$x+b,即可求得b的值;
(2)根据题意可以求点B的坐标,然后根据点C在y轴上,且△ABC的面积是2,即可求得点C的坐标.
解答 解:(1)∵点A(m,2)在双曲线y=$\frac{4}{x}$上,
∴2=$\frac{4}{m}$,得m=2,
∵点A(2,2)直线y=$\frac{1}{2}$x+b上,
∴2=$\frac{1}{2}×2+b$,得b=1,
由上可得,m的值是2,b的值是1;
(2)∵直线y=$\frac{1}{2}$x+1与y轴交于点B,
∴当x=0时,y=1,
即点B的坐标为(0,1),
又∵点C在y轴上,且△ABC的面积是2,点A(2,2),
∴$\frac{BC×2}{2}=2$,得BC=2,
∴点C的纵坐标为:1+2=3或1-2=-1,
∴点C的坐标为(0,3)或(0,-1).
点评 本题考查反比例函数与一次函数的交点问题,解答本题的关键是明确题意,找出所求问题需要的条件,此种题型最好是动手画一下,再进行解答比较好.

练习册系列答案
相关题目
4.已知反比例函数y=$\frac{k}{x}$的图象过点A(1,-2),则k的值为( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
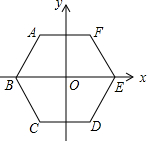 如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°.当n=2017时,顶点A的坐标为(2,2$\sqrt{3}$).
如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°.当n=2017时,顶点A的坐标为(2,2$\sqrt{3}$).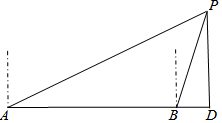 如图,一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向上,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.求灯塔P到轮船航线的距离PD是多少海里(结果保留根号)?
如图,一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向上,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.求灯塔P到轮船航线的距离PD是多少海里(结果保留根号)?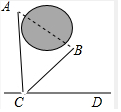 如图,A、B两个村庄之间有一个池塘,A村到公路CD的距离AC=700米,若BC═600米,∠BCD=30°,试求A、B两个村庄之间的距离(结果保留根号).
如图,A、B两个村庄之间有一个池塘,A村到公路CD的距离AC=700米,若BC═600米,∠BCD=30°,试求A、B两个村庄之间的距离(结果保留根号).
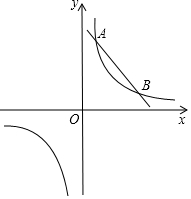 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图形交于A(a,4)和B(4,1)两点.
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图形交于A(a,4)和B(4,1)两点.