题目内容
15.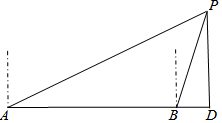 如图,一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向上,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.求灯塔P到轮船航线的距离PD是多少海里(结果保留根号)?
如图,一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向上,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.求灯塔P到轮船航线的距离PD是多少海里(结果保留根号)?
分析 过B作BC⊥PA于点C,根据正弦、余弦的定义求出BC、AC,根据等腰直角三角形的性质求出PC,得到AP,根据直角三角形的性质计算即可.
解答 解:过B作BC⊥PA于点C,
在Rt△ABC中,∠ACB=90°,∠BAC=30°,
∴BC=20,AC=20$\sqrt{3}$,
在Rt△PBC中,∠PCB=90°,∠BPC=45°,
∴PC=BC=20,
∴PA=20+20$\sqrt{3}$,
在Rt△APD中,∠ADP=90°,∠PAD=30°,
∴PD=10+10$\sqrt{3}$,
答:灯塔P到轮船航线的距离PD是(10+10$\sqrt{3}$)海里.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
 如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.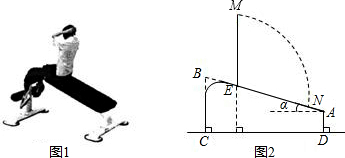
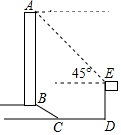 如图所示,广场有一纪念碑,其正前方恰有一个高度为15米的临时观侧台ED,从观测台顶端E处侧得纪念碑顶端A的仰角a是45°,观测台底端D到纪念碑底座边沿C的距离DC是20米,底座BC部分的坡长是12米,其坡度i=1:$\sqrt{3}$,求该纪念碑的高度.(结果精确到0.1米,参考数据:$\sqrt{2}≈1.41$,$\sqrt{3}≈1.73$,$\sqrt{6}≈2.45$)
如图所示,广场有一纪念碑,其正前方恰有一个高度为15米的临时观侧台ED,从观测台顶端E处侧得纪念碑顶端A的仰角a是45°,观测台底端D到纪念碑底座边沿C的距离DC是20米,底座BC部分的坡长是12米,其坡度i=1:$\sqrt{3}$,求该纪念碑的高度.(结果精确到0.1米,参考数据:$\sqrt{2}≈1.41$,$\sqrt{3}≈1.73$,$\sqrt{6}≈2.45$) 在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{4}{x}$的一个交点为A(m,2),与y轴分别交于点B.
在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{4}{x}$的一个交点为A(m,2),与y轴分别交于点B.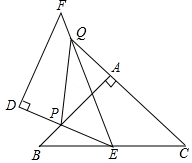 如图,△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.
如图,△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.