题目内容
2.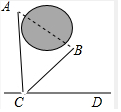 如图,A、B两个村庄之间有一个池塘,A村到公路CD的距离AC=700米,若BC═600米,∠BCD=30°,试求A、B两个村庄之间的距离(结果保留根号).
如图,A、B两个村庄之间有一个池塘,A村到公路CD的距离AC=700米,若BC═600米,∠BCD=30°,试求A、B两个村庄之间的距离(结果保留根号).
分析 作BH⊥AC于H.在Rt△ABH中,求出AH、BH即可利用勾股定理解决问题.
解答  解:作BH⊥AC于H.
解:作BH⊥AC于H.
∵AC⊥CD,∠BCD=30°,
∴∠BCH=60°,
在Rt△BCH中,BC=600米,∠BCH=60°,
∴CH=$\frac{1}{2}$BC=300米,BH=300$\sqrt{3}$米,
∵AC=700米,
∴AH=400米,
在Rt△AHB中,AB=$\sqrt{A{H}^{2}+B{H}^{2}}$=$\sqrt{40{0}^{2}+(300\sqrt{3})^{2}}$=100$\sqrt{43}$米.
答:A、B两个村庄之间的距离为100$\sqrt{43}$米.
点评 本题可知解直角三角形、锐角三角函数、勾股定理等知识,解题的关键是学会添加常用辅助线面构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
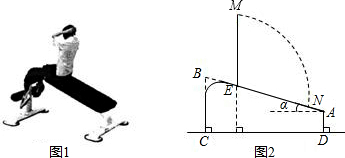
20. 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )
 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )| A. | 三棱柱 | B. | 三棱锥 | C. | 圆柱 | D. | 圆锥 |
17.一组数据:3、-1、0、2、-3、4,则这组数据的中位数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 2.5 |
 在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{4}{x}$的一个交点为A(m,2),与y轴分别交于点B.
在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{4}{x}$的一个交点为A(m,2),与y轴分别交于点B.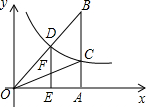 已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点C(3,1)
已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点C(3,1)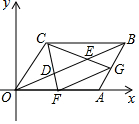 如图,平面直角坐标系中O是原点,?ABCD的顶点A,C的坐标分别是(8,0),(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:
如图,平面直角坐标系中O是原点,?ABCD的顶点A,C的坐标分别是(8,0),(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论: