题目内容
12.中考结束后,小亮乘坐“西宝高铁”回奶奶家过暑假,他发现座位后的小桌板收起时可近似看作与地面垂直,如图1,小桌板的支架底端C与桌面顶端的距离CA=75厘米,展开小桌板使桌面保持水平,如图2,此时OB⊥AC,∠ACB=△AOB=37°,且支架CB与桌面宽BO的长度之和等于CA的长度,求小桌板桌面的宽度BO.(结果精确到0.1cm,参考数据sin37°≈0.60,cos70°≈0.80,tan37°≈0.75)
分析 延长CB交AO于点D.则CD⊥OA,在Rt△OBD中根据正弦函数求得BD,根据余弦函数求得OD,在Rt△ACD中,根据正切函数求得AD,然后根据AD+OD=OA=75,列出关于x的方程,解方程即可求得.
解答  解:如图2,延长CB交AO于点D.
解:如图2,延长CB交AO于点D.
∴CD⊥OA,
设BC=x,则OB=75-x,
在Rt△OBD中,OD=OB•cos∠AOB,BD=OB•sin∠AOB,
∴OD=(75-x)•cos37°=0.8(75-x)=60-0.8x,
BD=(75-x)sin37°=0.6(75-x)=45-0.6x,
在Rt△ACD中,AD=DC•tan∠ACB,
∴AD=(x+45-0.6x)tan37°=0.75(0.4x+45)=0.3x+33.75,
∵AD+OD=OA=75,
∴0.3x+33.75+60-0.8x=75,
解得x=37.5.
∴BC=37.5,则BO=75-37.5=37.5(cm),
故小桌板桌面的宽度BO约为37.5cm.
点评 本题考查了解直角三角形的应用,解题的关键是正确构造直角三角形并求解.

练习册系列答案
相关题目
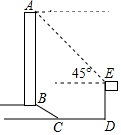 如图所示,广场有一纪念碑,其正前方恰有一个高度为15米的临时观侧台ED,从观测台顶端E处侧得纪念碑顶端A的仰角a是45°,观测台底端D到纪念碑底座边沿C的距离DC是20米,底座BC部分的坡长是12米,其坡度i=1:$\sqrt{3}$,求该纪念碑的高度.(结果精确到0.1米,参考数据:$\sqrt{2}≈1.41$,$\sqrt{3}≈1.73$,$\sqrt{6}≈2.45$)
如图所示,广场有一纪念碑,其正前方恰有一个高度为15米的临时观侧台ED,从观测台顶端E处侧得纪念碑顶端A的仰角a是45°,观测台底端D到纪念碑底座边沿C的距离DC是20米,底座BC部分的坡长是12米,其坡度i=1:$\sqrt{3}$,求该纪念碑的高度.(结果精确到0.1米,参考数据:$\sqrt{2}≈1.41$,$\sqrt{3}≈1.73$,$\sqrt{6}≈2.45$) 在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{4}{x}$的一个交点为A(m,2),与y轴分别交于点B.
在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{4}{x}$的一个交点为A(m,2),与y轴分别交于点B.