题目内容
16.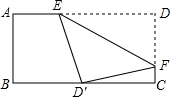 如图,将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合.若BC=6,CD=4,则CF=$\frac{7}{8}$.
如图,将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合.若BC=6,CD=4,则CF=$\frac{7}{8}$.
分析 根据折叠的性质知:DF=D′F,可在Rt△CFD′中,用CF的长表示出D′F,进而由勾股定理求得CF的值.
解答 解:∵D′是BC的中点,
∴D′C=$\frac{1}{2}$BC=3;
由折叠的性质知:DF=D′F,设CF=x,则D′F=DF=4-x;
在Rt△CFD′中,根据勾股定理得:D′F2=CF2+CD′2,即:
(4-x)2=x2+32,解得x=$\frac{7}{8}$;
故答案为:$\frac{7}{8}$.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后对应的边相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.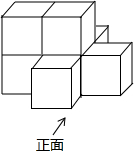 如图是一个由7个相同的小正方体搭成的几何体,这个几何体的主视图、左视图和俯视图中,是中心对称图形的是( )
如图是一个由7个相同的小正方体搭成的几何体,这个几何体的主视图、左视图和俯视图中,是中心对称图形的是( )
 如图是一个由7个相同的小正方体搭成的几何体,这个几何体的主视图、左视图和俯视图中,是中心对称图形的是( )
如图是一个由7个相同的小正方体搭成的几何体,这个几何体的主视图、左视图和俯视图中,是中心对称图形的是( )| A. | 主视图 | B. | 左视图 | C. | 俯视图 | D. | 左视图和俯视图 |
5.若将抛物线y=-x2先向右平移2个单位,再向上平移1个单位,则所得抛物线的表达式为( )
| A. | y=-(x-2)2-1 | B. | y=-(x-2)2-1 | C. | y=-(x+2)2-1 | D. | y=-(x-2)2+1 |
6.-6的相反数是( )
| A. | 6 | B. | -6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
 如图所示,已知2015是第k行的数字,则k等于673.
如图所示,已知2015是第k行的数字,则k等于673.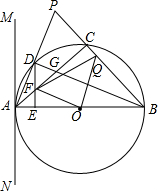 如图,已知△ABP是等腰三角形,AB=BP,以AB为直径的⊙O交AP于点D,交BP于点C,连接BD交AC于点G,直线MN过点A,且∠PAM=$\frac{1}{2}$∠ABP.
如图,已知△ABP是等腰三角形,AB=BP,以AB为直径的⊙O交AP于点D,交BP于点C,连接BD交AC于点G,直线MN过点A,且∠PAM=$\frac{1}{2}$∠ABP. 如图,CB是⊙O的切线,AF是⊙O的直径,CN⊥AF于点N,BG⊥AF于点G,连接AB交CN于点M.
如图,CB是⊙O的切线,AF是⊙O的直径,CN⊥AF于点N,BG⊥AF于点G,连接AB交CN于点M.