题目内容
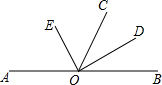 已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.
已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.(1)求∠EOD的度数;
(2)若∠AOE=50°,求∠BOC的度数.
考点:角平分线的定义
专题:
分析:(1)由于OE、OD分别平分∠AOC、∠BOC,所以∠EOC=
∠AOC,∠COD=
∠BOC,进而得出∠EOD=∠EOC+∠COD=
∠AOB=90°;
(2)由OE平分∠AOC,∠AOE=50°,得出∠AOC=2∠AOE=100°,再根据邻补角定义得出∠BOC=180°-∠AOC=80°.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由OE平分∠AOC,∠AOE=50°,得出∠AOC=2∠AOE=100°,再根据邻补角定义得出∠BOC=180°-∠AOC=80°.
解答:解:(1)∵OE、OD分别平分∠AOC、∠BOC,
∴∠EOC=
∠AOC,∠COD=
∠BOC,
∴∠EOD=∠EOC+∠COD=
∠AOC+
∠BOC=
∠AOB,
又∵A、O、B三点在同一直线上,
∴∠AOB=180°,
∴∠EOD=
∠AOB=90°;
(2)∵OE平分∠AOC,∠AOE=50°,
∴∠AOC=2∠AOE=100°,
∴∠BOC=180°-∠AOC=80°.
∴∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOD=∠EOC+∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵A、O、B三点在同一直线上,
∴∠AOB=180°,
∴∠EOD=
| 1 |
| 2 |
(2)∵OE平分∠AOC,∠AOE=50°,
∴∠AOC=2∠AOE=100°,
∴∠BOC=180°-∠AOC=80°.
点评:本题考查了角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.也考查了角的和差,邻补角定义,准确识图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知线段AB,请用尺规按下列要求作图.
如图,已知线段AB,请用尺规按下列要求作图. 在Rt△ABC中,∠C=90°,cosB=
在Rt△ABC中,∠C=90°,cosB=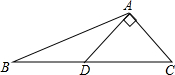 如图,在△ABC中,∠BAC=120°,AD⊥AC,D为BC中点,求tanC和cosC的值.
如图,在△ABC中,∠BAC=120°,AD⊥AC,D为BC中点,求tanC和cosC的值.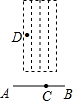 如图,田径运动会上,七年级二班的小亮同学从点C起跳,假若落地点是D,且线段CD的长度是一定的,则当AB与CD
如图,田径运动会上,七年级二班的小亮同学从点C起跳,假若落地点是D,且线段CD的长度是一定的,则当AB与CD