题目内容
 如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若CD=1,且∠AEC=30°,求BE的长.
考点:切线的判定
专题:
分析:(1)连接OC,可证明OC∥AD,可证明CD为⊙O的切线;
(2)连接BC,可证得BC=BE,再根据含30°角的直角三角形的性质,可求得BC,可得出BE的长.
(2)连接BC,可证得BC=BE,再根据含30°角的直角三角形的性质,可求得BC,可得出BE的长.
解答:解:(1)CD与⊙O相切,理由如下:
如图1,连接OC,
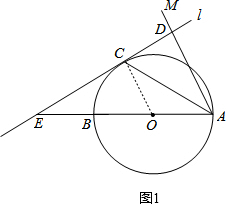
∵OC=OA,
∴∠OCA=∠BAC,
又∵∠BAC=∠CAM,
∴∠OCA=∠CAM,
∴OC∥AM,
∵AM⊥CD,
∴∠ECO=∠CDA=90°,
∴OC⊥CD,
∴CD与⊙O相切;
(2)如图2,连接BC,
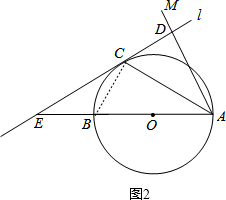
∵∠AEC=30°,∠CDA=90°,
∴∠BAD=60°,
∴∠CAB=∠CAD=30°,
∵AB为⊙O的直径,
∴∠BCA=90°,
∴∠BCE=30°,
∴BE=BC,
在Rt△ACD中,CD=1,∠CAD=30°,
∴AC=2CD=2,
在Rt△ABC中,AC=2,∠BAC=30°,
∴BC=AC•tan∠BAC=2×
=
,
∴BE=
.
如图1,连接OC,

∵OC=OA,
∴∠OCA=∠BAC,
又∵∠BAC=∠CAM,
∴∠OCA=∠CAM,
∴OC∥AM,
∵AM⊥CD,
∴∠ECO=∠CDA=90°,
∴OC⊥CD,
∴CD与⊙O相切;
(2)如图2,连接BC,

∵∠AEC=30°,∠CDA=90°,
∴∠BAD=60°,
∴∠CAB=∠CAD=30°,
∵AB为⊙O的直径,
∴∠BCA=90°,
∴∠BCE=30°,
∴BE=BC,
在Rt△ACD中,CD=1,∠CAD=30°,
∴AC=2CD=2,
在Rt△ABC中,AC=2,∠BAC=30°,
∴BC=AC•tan∠BAC=2×
| ||
| 3 |
2
| ||
| 3 |
∴BE=
2
| ||
| 3 |
点评:本题主要考查切线的判定和性质,掌握切线的两种证明方法是解题的关键,即①有切点时,连接圆心和切点,证明垂直,②当没有切点时,作垂直,证明距离等于半径.

练习册系列答案
相关题目
若A、O、B三点在同一条直线上,OA=3,OB=5,则A、B两点间的距离为( )
| A、2 | B、8 | C、3 | D、8或2 |
 如图,AB是一段火车行驶路线图,图中字母所示的5个点表示5个车站,在这段路线上往返行车,需印制( )种车票.
如图,AB是一段火车行驶路线图,图中字母所示的5个点表示5个车站,在这段路线上往返行车,需印制( )种车票.| A、21 | B、42 | C、6 | D、12 |
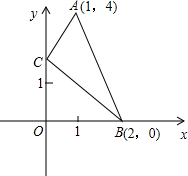 在平面直角坐标系中,已知两点A(1,4)B(2,0),点C是y轴上的一个动点,且A、B、C三点不共线,求△ABC周长的最小值及相应点C的坐标.
在平面直角坐标系中,已知两点A(1,4)B(2,0),点C是y轴上的一个动点,且A、B、C三点不共线,求△ABC周长的最小值及相应点C的坐标.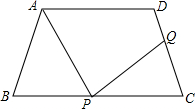 如图,在梯形ABCD中,∠ABC=∠DCB,AB=DC=6cm,BC=8cm,若点P从点B开始沿BC方向运动,同时点Q从点C开始沿CD方向运动,速度不一样,当它们的速度比是多少时,以A、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等?
如图,在梯形ABCD中,∠ABC=∠DCB,AB=DC=6cm,BC=8cm,若点P从点B开始沿BC方向运动,同时点Q从点C开始沿CD方向运动,速度不一样,当它们的速度比是多少时,以A、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等? 如图,点C在AB上,点M、N分别是AC、BC的中点,
如图,点C在AB上,点M、N分别是AC、BC的中点, 如图,∠AOC和∠DOB都是直角,如果∠DOC=26°,那么∠AOB的度数是
如图,∠AOC和∠DOB都是直角,如果∠DOC=26°,那么∠AOB的度数是 在Rt△ABC中,∠C=90°,cosB=
在Rt△ABC中,∠C=90°,cosB=