题目内容
已知关于x的方程kx2+(k+2)x+
=0有两个不相等实根.
(1)求k的取值范围;
(2)是否存在实数k,使方程的两个实根的倒数和等于零?若存在,求出k的值,若不存在,请说明理由.
| k |
| 2 |
(1)求k的取值范围;
(2)是否存在实数k,使方程的两个实根的倒数和等于零?若存在,求出k的值,若不存在,请说明理由.
考点:根的判别式,一元二次方程的定义,根与系数的关系
专题:
分析:(1)由于方程有两个不相等的实数根,令△>0且k≠0即可;
(2)令
+
=0,建立关于k的方程,解答即可.
(2)令
| 1 |
| x1 |
| 1 |
| x2 |
解答:解:(1)∵方程kx2+(k+2)x+
=0有两个不相等实根,
∴
,
解得k>2+2
或k<2-2
.
(2)设方程两根为x1、x2,
∵
+
=0,
∴
=0,
∴
=0,
∴k=-1或k=-3.
| k |
| 2 |
∴
|
解得k>2+2
| 2 |
| 2 |
(2)设方程两根为x1、x2,
∵
| 1 |
| x1 |
| 1 |
| x2 |
∴
| (x1+x2)2-2x1x2 |
| x1x2 |
∴
(-
| ||||
|
∴k=-1或k=-3.
点评:本题考查了根的判别式、一元二次方程的定义、根与系数的关系,综合性较强,计算难度较大,需特别关注.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
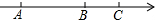 如图,在数轴上(未标出原点及单位长度)点B为线段AC的中点,已知点A、B、C对应的三个数a、b、c之积是负数,这三个数之和与其中一数相等,设p为a、b、c三数中两数的比值,求p的最大值和最小值.
如图,在数轴上(未标出原点及单位长度)点B为线段AC的中点,已知点A、B、C对应的三个数a、b、c之积是负数,这三个数之和与其中一数相等,设p为a、b、c三数中两数的比值,求p的最大值和最小值.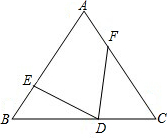 如图所示,△ABC是等边三角形,点D,E,F分别是边BC,AB,AC边上的点,且BE=CD,∠EDF=60°,求证:ED=FD.
如图所示,△ABC是等边三角形,点D,E,F分别是边BC,AB,AC边上的点,且BE=CD,∠EDF=60°,求证:ED=FD.