题目内容
用篱笆围成的一个长方形菜地，其中一面靠墙，且与墙平行的一边开一扇2米宽的门，如果墙长50米，现有91米长的篱笆，菜地的面积需要1080平方米，求菜地长和宽．
考点：一元二次方程的应用
专题：几何图形问题
分析：设出一边的长，然后表示出另一边的长，利用面积的公式列出方程求解即可．
解答：解：设一边为x米，则另一边长为（93-2x）米，根据题意得：
x（93-2x）=1080，
解得：x=48（舍去）或x=45，
则93-2x=93-90=3．
答：长为45米，宽为3米．
x（93-2x）=1080，
解得：x=48（舍去）或x=45，
则93-2x=93-90=3．
答：长为45米，宽为3米．
点评：本题考查了一元二次方程的应用，解题的关键是根据一边表示出另一边的长，难度不大．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
计算：
（1）（-7）+（+10）+（-1）+（-2）
（2）-22×7-（-3）×6-5÷（-
）
（3）4x2y-8xy2+7-4x2y+10xy2-4
（4）3（2x2-xy）-4（x2-xy-6）
（1）（-7）+（+10）+（-1）+（-2）
（2）-22×7-（-3）×6-5÷（-
| 1 |
| 5 |
（3）4x2y-8xy2+7-4x2y+10xy2-4
（4）3（2x2-xy）-4（x2-xy-6）
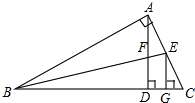如图所示，在Rt△ABC中，AD是斜边上的高，∠ABC的平分线分别交AD、AC于点F、E，EG⊥BC于G，下列结论正确的是（ ）| A、∠C=∠ABC |
| B、BA=BG |
| C、AE=CE |
| D、AF=FD |
已知等边△ABC中，D为AC上一点，以DC为边作等边△CDE，连接AE，交BD的延长线与点F，连接CF．