Question

14．数学思考：（1）如图1，已知AB∥CD，探究下面图形中∠APC和∠PAB、∠PCD的关系，并证明你的结论
推广延伸：（2）①如图2，已知AA₁∥BA₁，请你猜想∠A₁，∠B₁，∠B₂，∠A₂、∠A₃的关系，并证明你的猜想；
②如图3，已知AA₁∥BA_n，直接写出∠A₁，∠B₁，∠B₂，∠A₂、…∠B_n-1、∠A_n的关系
拓展应用：（3）①如图4所示，若AB∥EF，用含α，β，γ的式子表示x，应为B
A.180°+α+β-γ       B.180°-α-γ+β　       C．β+γ-α　      D．α+β+γ　
②如图5，AB∥CD，且∠AFE=40°，∠FGH=90°，∠HMN=30°，∠CNP=50°，请你根据上述结论直接写出∠GHM的度数是30°．

Answer 1

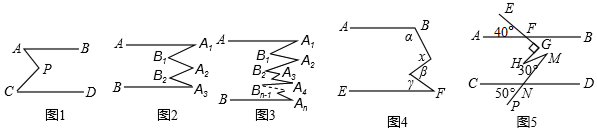
分析 （1）过点P作OP∥AB，根据两直线平行，内错角相等可得∠1=∠PAB，∠2=∠PCD，再根据∠APC=∠1+∠2整理即可得证；
（2）①过点A₂作A₂O∥AA₁，根据（1）可得∠B₁=∠A₁+∠1，∠B₂=∠2+∠A₃，然后相加整理即可得解；②根据规律，A系列的角的和等于B系列的角的和列式即可；
（3）①过∠x的顶点作CD∥AB，然后根据平行线的性质和（1）的结论表示出x即可；②根据（2）的结论列式计算即可得解．

解答 解：（1）证明：如图1，过点P作OP∥AB，
∵AB∥CD，
∴OP∥AB∥CD，
∴∠1=∠PAB，∠2=∠PCD，
∴∠APC=∠1+∠2=∠PAB+∠PCD，
即∠APC=∠PAB+∠PCD；

（2）①如图2，过点A₂作A₂O∥AA₁，
由（1）可知∠B₁=∠A₁+∠1，∠B₂=∠2+∠A₃，
所以，∠B₁+∠B₂=∠A₁+∠A₂+∠A₃；
②如图3，由①可知：
∠A₁+∠A₂+…+∠A_n=∠B₁+∠B₂+…+∠B_n-1；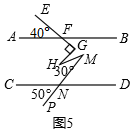

（3）①如图4，过∠x的顶点作CD∥AB，
则∠x=（180°-α）+（β-γ）=180°-α-γ+β，
②如图5，由（1）可知，40°+∠GHM+50°=∠G+∠M，
∵∠G=90°，∠M=30°，
∴∠GHM=90°+30°-40°-50°=30°．
故答案为：B；30°．

点评 本题考查了平行线的性质，熟练掌握性质并作出辅助线是解题的关键，难点在于总结出A系列的角的和等于B系列的角的和．