题目内容
19．
如图，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD=120°，AB=2，则AC的长为（ ）| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
分析 只要证明△AOB是等边三角形即可解决问题．
解答 解：∵四边形ABCD是矩形，
∴AC=BD，OA=OC，OB=OD，
∴OA=OB，
∵∠AOD=120°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴OA=OB=AB=2，
∴AC=2OA=4，
故选B．
点评 本题考查矩形的性质、等边三角形的判定和性质等知识，解题的关键是熟练掌握矩形的性质，属于中考常考题型．
练习册系列答案
名校课堂系列答案
相关题目
9．
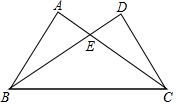如图，已知△ABC≌△DCB，AB=10，∠A=60°，∠ABC=80°，那么下列结论中错误的是（ ）
如图，已知△ABC≌△DCB，AB=10，∠A=60°，∠ABC=80°，那么下列结论中错误的是（ ）| A． | ∠D=60° | B． | ∠DBC=40° | C． | AC=DB | D． | BE=10 |
10．下列式子中，表示y是x的正比例函数的是（ ）
| A． | y=x-1 | B． | y=2x | C． | y=2x2 | D． | y2=2x |
7．在实数-2，0，-$\sqrt{3}$，1中，最小的数是（ ）
| A． | -2 | B． | 0 | C． | -$\sqrt{3}$ | D． | 1 |
4．设n为正整数，且n＜$\sqrt{62}$＜n+1，则n的值为（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
11．若m＜n，则下列不等式中，正确的是（ ）
| A． | m-4＞n-4 | B． | $\frac{m}{5}$＞$\frac{n}{5}$ | C． | 2m+1＜2n+1 | D． | -3m＜-3n |
8．
如图，在△ABC中，AB=AC，点D，E分别在边BC 和AC上，若AD=AE，则下列结论错误的是（ ）
如图，在△ABC中，AB=AC，点D，E分别在边BC 和AC上，若AD=AE，则下列结论错误的是（ ）| A． | ∠ADB=∠ACB+∠CAD | B． | ∠ADE=∠AED | C． | ∠CDE=$\frac{1}{2}$∠BAD | D． | ∠AED=2∠ECD |
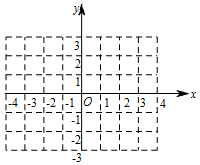已知一次函数y=-$\frac{1}{2}$x+1，它的图象与x轴交于点A，与y轴交于点B．