题目内容
2. 如图,点E在以AB为直径的⊙O上,点C是$\widehat{BE}$的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
如图,点E在以AB为直径的⊙O上,点C是$\widehat{BE}$的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.(1)求证:CD是⊙O的切线;
(2)若cos∠CAD=$\frac{4}{5}$,BF=15,求AC的长.
分析 (1)连接OC,由点C是$\widehat{BE}$的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.
(2)过点O作OM⊥AC于点M,由点C是$\widehat{BE}$的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD=$\frac{4}{5}$可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
解答 (1)证明:连接OC,如图1所示.
∵点C是$\widehat{BE}$的中点,
∴$\widehat{CE}$=$\widehat{BC}$,
∴OC⊥BE.
∵AB是⊙O的直径,
∴AD⊥BE,
∴AD∥OC.
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线.
(2)解:过点O作OM⊥AC于点M,如图2所示.
∵点C是$\widehat{BE}$的中点,
∴$\widehat{CE}$=$\widehat{BC}$,∠BAC=∠CAE,
∴$\frac{EF}{AE}$=$\frac{BF}{AB}$.
∵cos∠CAD=$\frac{4}{5}$,
∴$\frac{EF}{AE}$=$\frac{3}{4}$,
∴AB=$\frac{4}{3}$BF=20.
在Rt△AOM中,∠AMO=90°,AO=$\frac{1}{2}$AB=10,cos∠OAM=cos∠CAD=$\frac{4}{5}$,
∴AM=AO•cos∠OAM=8,
∴AC=2AM=16.
点评 本题考查了切线的判定与性质、解直角三角形、平行线的性质、垂径定理、圆周角定理以及角平分线的性质,解题的关键是:(1)根据平行线的性质找出OC⊥CD;(2)根据角平分线的性质求出AB的长度.

| A. | 12cm | B. | 10cm | C. | 8cm | D. | 5cm |
| A. | y=x-1 | B. | y=2x | C. | y=2x2 | D. | y2=2x |
| A. | -2 | B. | 0 | C. | -$\sqrt{3}$ | D. | 1 |
| A. | m-4>n-4 | B. | $\frac{m}{5}$>$\frac{n}{5}$ | C. | 2m+1<2n+1 | D. | -3m<-3n |
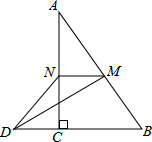 如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=$\frac{1}{2}$BC,连接DM,DN,MN,若AB=6,则DN=3.
如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=$\frac{1}{2}$BC,连接DM,DN,MN,若AB=6,则DN=3. 如图,是药品研究所所测得的某种新药在成人用药后,血液中的药物浓度y(微克/毫升)随用药后的时间x(小时)变化的图象(图象由线段OA与部分双曲线AB组成).并测得当y=a时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物就失去疗效,那么成人用药后需要多长时间血液中药物浓度才能达到最大值?
如图,是药品研究所所测得的某种新药在成人用药后,血液中的药物浓度y(微克/毫升)随用药后的时间x(小时)变化的图象(图象由线段OA与部分双曲线AB组成).并测得当y=a时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物就失去疗效,那么成人用药后需要多长时间血液中药物浓度才能达到最大值?