题目内容
2.根据如图数轴表示,化简下式:|a+$\sqrt{2}$|-$\sqrt{(\sqrt{3}-b)^{2}}$-$\sqrt{(\sqrt{2}-b)^{2}}$.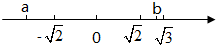
分析 根据数轴确定a、b的范围,根据二次根式的性质把原式去掉绝对值和二次根号,合并同类二次根式即可.
解答 解:由数轴可知,a<-$\sqrt{2}$,$\sqrt{2}$<b<$\sqrt{3}$,
则a+$\sqrt{2}$<0,$\sqrt{3}$-b>0,$\sqrt{2}$-b<0,
原式=-(a+$\sqrt{2}$)-($\sqrt{3}$-b)+($\sqrt{2}$-b)
=-a-$\sqrt{2}$-$\sqrt{3}$+b+$\sqrt{2}$-b
=-a-$\sqrt{3}$.
点评 本题考查的是数轴、实数的大小比较以及二次根式的化简求值,掌握数轴上实数的大小比较法则、正确运用二次根式的性质是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
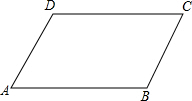 如图,已知平行四边形ABCD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示下列向量:
如图,已知平行四边形ABCD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示下列向量: 如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.
如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.