题目内容
3.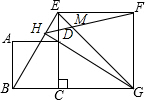 如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.
如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.
分析 取EG中点O,连接OH,先证明△BCE≌△DCG推出HG⊥BE,再证明△BGH≌△EGH,推出OH是三角形中位线,设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,利用△DHN∽△DGC,得$\frac{DN}{DC}$=$\frac{HN}{CG}$,求出a、b之间的关系,最后由△EFM∽△OMH,得$\frac{EM}{OM}$=$\frac{EF}{OH}$=$\frac{2b}{a+b}$,推出$\frac{EM}{MG}$=$\frac{b}{a+2b}$=$\frac{1}{\frac{a}{b}+2}$即可解决问题.
解答 解:取EG中点O,连接OH
∵四边形ABCD是正方形,
∴BC=DC,∠BCE=90°,
同理可得CE=CG,∠DCG=90°,
在△BCE和△DCG中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCE=∠DCG=90°}\\{CE=CG}\end{array}\right.$,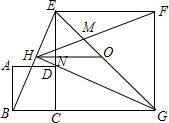
∴△BCE≌△DCG,
∴∠BEC=∠DGC,
∵∠EDH=∠CDG,∠DGC+∠CDG=90°,
∴∠EDH+∠BEC=90°,
∴∠EHD=90°,
∴HG⊥BE,
在△BGH和△EGH中,
$\left\{\begin{array}{l}{∠EHG=∠BHG}\\{HG=HG}\\{∠EGH=∠BGH}\end{array}\right.$,
∴△BGH≌△EGH,
∴BH=EH,
∵EH=HB,EO=OG,
∴HO∥BG,HO=$\frac{1}{2}$BG=$\frac{1}{2}$EF,
设EC和OH相交于点N.
设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,
∵OH∥BC,
∴△DHN∽△DGC,
∴$\frac{DN}{DC}$=$\frac{HN}{CG}$,即$\frac{b-2a}{2a}$=$\frac{a}{2b}$,即a2+2ab-b2=0,
解得:a=(-1+$\sqrt{2}$)b,或a=(-1-$\sqrt{2}$)b(舍去),
则$\frac{a}{b}$=$\sqrt{2}$-1,
∵EF∥OH,
∴△EFM∽△OMH,
∴$\frac{EM}{OM}$=$\frac{EF}{OH}$=$\frac{2b}{a+b}$,
∴$\frac{EM}{OE}$=$\frac{2b}{a+3b}$,$\frac{EM}{EG}$=$\frac{b}{a+3b}$,
∴$\frac{EM}{MG}$=$\frac{b}{a+2b}$=$\frac{1}{\frac{a}{b}+2}$=$\frac{1}{\sqrt{2}-1+2}$=$\frac{1}{\sqrt{2}+1}$,
∴$\frac{MG}{ME}$=$\sqrt{2}$+1.
故答案为$\sqrt{2}+1$.
点评 本题考查了正方形的性质,以及全等三角形的判定与性质,相似三角形的判定与性质,正确求得两个三角形的边长的比是解决本题的关键,题目比较难.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.
如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象的点,连结OA,作OA⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B. 如图,将一张长方形纸片的一角斜折过去,使角的顶点A落在A′处,BC为折痕,若BD平分∠A′BE,则BC与BD的位置关系是垂直.
如图,将一张长方形纸片的一角斜折过去,使角的顶点A落在A′处,BC为折痕,若BD平分∠A′BE,则BC与BD的位置关系是垂直.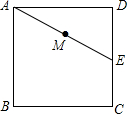 如图,已知正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.若PQ=AE,则AP=$\frac{5}{2}$或$\frac{3}{2}$cm.
如图,已知正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.若PQ=AE,则AP=$\frac{5}{2}$或$\frac{3}{2}$cm. 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车匀速行驶(汽车速度大于摩托车的速度);甲先到达B地停留半个小时后返回A地,如图是他们之间的距离y(千米)与甲出发时间x(小时)之间的函数图象,其中D表示甲返回到A地.
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车匀速行驶(汽车速度大于摩托车的速度);甲先到达B地停留半个小时后返回A地,如图是他们之间的距离y(千米)与甲出发时间x(小时)之间的函数图象,其中D表示甲返回到A地.
