题目内容
20.直线y=kx+b与直线y=2x交于点A(1,m),且经过点B(-2,6),则此函数解析式为y=-$\frac{4}{3}$x+$\frac{10}{3}$.分析 可先求出点A的坐标,然后运用待定系数法就可解决问题.
解答 解:∵点A(1,m)在直线y=2x上,
∴m=2×1=2,
∴点A的坐标为(1,2).
∵点A(1,2)、B(-2,6)在直线y=kx+b上,
∴$\left\{\begin{array}{l}{k+b=2}\\{-2k+b=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=\frac{10}{3}}\end{array}\right.$,
∴该函数的解析式为y=-$\frac{4}{3}$x+$\frac{10}{3}$.
故答案为y=-$\frac{4}{3}$x+$\frac{10}{3}$.
点评 本题主要考查了直线上点的坐标特征、运用待定系数法求一次函数的解析式、解二元一次方程组等知识,运用待定系数法是求函数解析式常用的方法,应熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
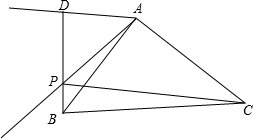 在△ABC中,∠BAC=90°,作∠DAP=∠ABC=45°,过点B作BD⊥AD,垂足为D,BD交直线AP于P.
在△ABC中,∠BAC=90°,作∠DAP=∠ABC=45°,过点B作BD⊥AD,垂足为D,BD交直线AP于P. 如图,在四边形ABCD中,AB=AC,∠ABC=60°,∠ADC=30°,求证:DB2=DC2+DA2.
如图,在四边形ABCD中,AB=AC,∠ABC=60°,∠ADC=30°,求证:DB2=DC2+DA2. 如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.