题目内容

12．在△ABC中，若AB=4$\sqrt{3}$，AC=4，∠B=30°，则S△ABC=8$\sqrt{3}$．

分析 根据含30°的直角三角形的性质解答即可．

解答 解：因为AB=4$\sqrt{3}$，AC=4，∠B=30°，
所以BC=$\sqrt{（4\sqrt{3}）^{2}+{4}^{2}}=8$，
所以S△ABC=$\frac{1}{2}×4×4\sqrt{3}=8\sqrt{3}$，
故答案为：8$\sqrt{3}$

点评 此题考查解直角三角形问题，关键根据已知得出三角形ABC是直角三角形解答．

练习册系列答案
相关题目
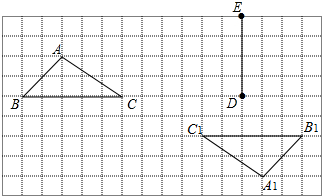2．在如图的方格纸中，每个小正方形的边长都为1，△ABC与△A1B1C1构成的图形是中心对称图形．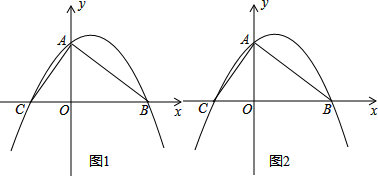
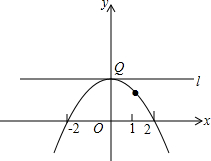（1）画出此中心对称图形的对称中心O；
（2）画出将△A1B1C1沿直线DE方向向上平移5格得到的△A2B2C2；
（3）求出△CC1C2的面积．
3．计算：
（1）$\frac{c}{a{b}^{2}}$$+\frac{bc}{a{b}^{2}}$；
（2）$\frac{3}{a}+\frac{a-15}{5a}$；
（3）$\frac{1}{{R}_{1}}$$+\frac{1}{{R}_{2}}$；
（4）$\frac{b}{a+b}$$+\frac{ab}{{b}^{2}-{a}^{2}}$．
20．直线y=kx+b与直线y=2x交于点A（1，m），且经过点B（-2，6），则此函数解析式为y=-$\frac{4}{3}$x+$\frac{10}{3}$．
7．关于x的方程kx2-2x-1=0有两个实数根x1，x2．
（1）求k的取值范围；
（2）若（x1+1）（x2+1）=$\frac{4}{9}$k，求k的值．
5．如图抛物线y=ax2+bx+c经过A、B、C三点，连接AB、AC，AB=2$\sqrt{13}$，tan∠ABC=$\frac{2}{3}$，S△ABC=20．
（1）求此抛物线的解析式；
（2）点D为x轴上方抛物线上一点，过点D作DE⊥x轴，垂足为点E，交线段AB于点F．当FD=FE时，求点E的坐标；
（3）在（2）的条件下，点P为射线AE上一动点，连接CP交y轴于点M，连接ME，并过点M作AE的平行线，过点E作ME的垂线，这两条直线相交于点N．当△MEN中有一个角的正切值为$\frac{1}{2}$时，求出点P坐标，并判断点P是否在（1）中的抛物线上．
12．在平面直角坐标系xOy中，已知二次函数y=-$\frac{1}{4}{x}^{2}+mx+n$的图象经过点A（2，0）和点B（1，$\frac{3}{4}$），直线l经过抛物线的顶点且与y轴垂直，垂足为Q．
（1）求该二次函数的表达式；
（2）设抛物线上有一动点P从点B处出发沿抛物线向下运动，其纵坐标y1随时间t（t≤0）的变化规律为y1=$\frac{3}{4}$-2t．设点C是线段OP的中点，作DC⊥l于点D．
①点P运动的过程中，$\frac{CD}{OP}$是否为定值，请说明理由；
②若在点P开始运动的同时，直线l也向下平行移动，且垂足Q的纵坐标y2随时间t的变化规律为y2=1-3t，以OP为直径作⊙C，l与⊙C的交点为E、F，若EF=$\sqrt{3}$，求t的值．
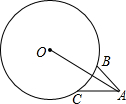9．如图，△ABC中，BC=4，∠BAC=45°，以$4\sqrt{2}$为半径，过B、C两点作⊙O，连OA，则线段OA的最大值为2$\sqrt{2}$+2+2$\sqrt{7}$．
10．计算：
（1）$\root{3}{27}$-$\sqrt{4}$+（$\sqrt{3}$）2
（2）$\frac{\sqrt{20}+\sqrt{5}}{\sqrt{5}}$-2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网