题目内容
18. 如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.(1)求证:△ACD是等边三角形;
(2)若DE=1,求圆O的半径.
分析 (1)由BM⊥AB,CD∥BM,得到CD⊥AB,而AB是⊙O的直径,根据垂径定理得到$\widehat{AD}$=$\widehat{AC}$,于是得到AD=AC,然后根据已知DA=DC,得出AD=AC=CD,即可证明△ACD是等边三角形;
(2)连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,得到∠DAC=60°又直角三角形的性质得到BE=$\frac{1}{2}$AE,ON=$\frac{1}{2}$AO,设⊙O的半径为r,则ON=$\frac{1}{2}$r,AN=DN=$\frac{\sqrt{3}}{2}$r,由于得到EN=1+$\frac{\sqrt{3}}{2}$r,BE=$\frac{1}{2}$AE=$\frac{\sqrt{3}r+1}{2}$,在Rt△ONE与Rt△BEO中,由勾股定理列方程即可求解.
解答 (1)证明:∵BM⊥AB,CD∥BM,
∴AB⊥CD,
∵AB是⊙O的直径,
∴$\widehat{AD}$=$\widehat{AC}$,
∴AD=AC,
∵DA=DC,
∴AD=AC=CD,
∴△ACD是等边三角形;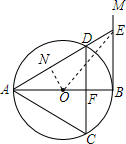 (2)解:连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,
(2)解:连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,
∴∠DAC=60°.
∵AD=AC,CD⊥AB,
∴∠DAB=30°,
∴BE=$\frac{1}{2}$AE,ON=$\frac{1}{2}$AO,
设⊙O的半径为r,
∴ON=$\frac{1}{2}$r,AN=DN=$\frac{\sqrt{3}}{2}$r,
∴EN=1+$\frac{\sqrt{3}}{2}$r,BE=$\frac{1}{2}$AE=$\frac{\sqrt{3}r+1}{2}$.
在Rt△ONE与Rt△BEO中,
OE2=ON2+NE2=OB2+BE2,
即($\frac{1}{2}$r)2+(1+$\frac{\sqrt{3}}{2}$r)2=r2+($\frac{\sqrt{3}r+1}{2}$)2,
解得r1=$\sqrt{3}$,r2=-$\frac{\sqrt{3}}{3}$(不合题意舍去).
故圆O的半径为$\sqrt{3}$.
点评 本题考查了切线的性质,垂径定理,等边三角形的判定,直角三角形的性质,勾股定理,过O作ON⊥AD于N,构造直角三角形是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 30cm | B. | 50cm | C. | 60cm | D. | 120cm |
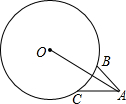 如图,△ABC中,BC=4,∠BAC=45°,以$4\sqrt{2}$为半径,过B、C两点作⊙O,连OA,则线段OA的最大值为2$\sqrt{2}$+2+2$\sqrt{7}$.
如图,△ABC中,BC=4,∠BAC=45°,以$4\sqrt{2}$为半径,过B、C两点作⊙O,连OA,则线段OA的最大值为2$\sqrt{2}$+2+2$\sqrt{7}$. ”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
 表示的自然数是18;
表示的自然数是18; .
.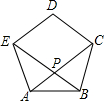 己知:如图,正五边形的对角线AC和BE相交于点P.求证:
己知:如图,正五边形的对角线AC和BE相交于点P.求证: