题目内容
17. 如图,在四边形ABCD中,AB=AC,∠ABC=60°,∠ADC=30°,求证:DB2=DC2+DA2.
如图,在四边形ABCD中,AB=AC,∠ABC=60°,∠ADC=30°,求证:DB2=DC2+DA2.
分析 要证明DB2=DC2+DA2,想到勾股定理,由于BD,AD,DC不在同一个三角形中,连接AC,将△DAB绕点A旋转60°到△ACE的位置,连接ED,证明△CDE是直角三角形即可.
解答 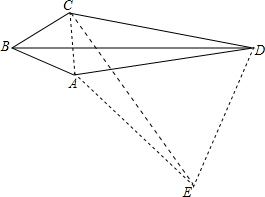 证明:如图,连接AC,
证明:如图,连接AC,
∵AB=CB,∠ABC=60°,
∴△ABC是正三角形.
∴BC=CA=AB.
将△DAB绕点A顺时针旋转60°到△ACE的位置,连接ED,
∴DA=AE,BD=CE,∠DAE=∠CAE-∠CAD=∠BAD-∠CAD=∠BAC=60°,
∴△DAE为正三角形.
∴DE=AD,∠ADE=60°.
∴∠CDE=∠CDA+∠ADE=90°.
在Rt△CDE中,由勾股定理得CE2=CD2+DE2.
∴DB2=DC2+DA2.
点评 此题主要考查了全等三角形的判定与性质,能够充分运用旋转的性质,把要证明的线段转换到一个三角形中,根据旋转的性质发现一个直角三角形,再根据勾股定理即可证明.

练习册系列答案
相关题目
7.李师傅做了一个三角形的工件,其中两条边长分别为30cm和80cm,则另一边长度可能是( )
| A. | 30cm | B. | 50cm | C. | 60cm | D. | 120cm |
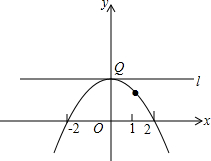 在平面直角坐标系xOy中,已知二次函数y=-$\frac{1}{4}{x}^{2}+mx+n$的图象经过点A(2,0)和点B(1,$\frac{3}{4}$),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.
在平面直角坐标系xOy中,已知二次函数y=-$\frac{1}{4}{x}^{2}+mx+n$的图象经过点A(2,0)和点B(1,$\frac{3}{4}$),直线l经过抛物线的顶点且与y轴垂直,垂足为Q. 如图,△ABC内接于圆,点D是AC上一点,将∠A沿BD翻折,点A正好落在圆上点E处.若∠C=50°,则∠ABE的度数为80°.
如图,△ABC内接于圆,点D是AC上一点,将∠A沿BD翻折,点A正好落在圆上点E处.若∠C=50°,则∠ABE的度数为80°.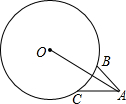 如图,△ABC中,BC=4,∠BAC=45°,以$4\sqrt{2}$为半径,过B、C两点作⊙O,连OA,则线段OA的最大值为2$\sqrt{2}$+2+2$\sqrt{7}$.
如图,△ABC中,BC=4,∠BAC=45°,以$4\sqrt{2}$为半径,过B、C两点作⊙O,连OA,则线段OA的最大值为2$\sqrt{2}$+2+2$\sqrt{7}$.