题目内容
10. 如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )| A. | 10 | B. | 8$\sqrt{2}$ | C. | 2$\sqrt{17}$ | D. | 8 |
分析 要使DN+MN最小,首先应分析点N的位置.根据正方形的性质:正方形的对角线互相垂直平分.知点D的对称点是点B,连接MB交AC于点N,此时DN+MN最小值即是BM的长.
解答 解:根据题意,连接BD、BM,则BM就是所求DN+MN的最小值,
在Rt△BCM中,BC=8,CM=6
根据勾股定理得:BM=$\sqrt{{6}^{2}+{8}^{2}}$=10,
即DN+MN的最小值是10;
故选A.
点评 此题考查轴对称问题,此题的难点在于确定满足条件的点N的位置:利用轴对称的方法.然后熟练运用勾股定理.

练习册系列答案
相关题目
20.下列图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.直线y=-$\frac{2}{3}$x+$\frac{1}{2}$不经过的象限是( )
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
5.?ABCD中,∠A=30°,AB边上的高为6,则BC的长为( )
| A. | 12 | B. | 6 | C. | 6$\sqrt{2}$ | D. | 6$\sqrt{3}$ |
15.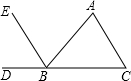 如图,能判定EB∥AC的是( )
如图,能判定EB∥AC的是( )
 如图,能判定EB∥AC的是( )
如图,能判定EB∥AC的是( )| A. | ∠C=∠ABE | B. | ∠A=∠EBD | C. | ∠C=∠ABC | D. | ∠A=∠ABE |
19. 如图,下列条件能判定AD∥BC的是( )
如图,下列条件能判定AD∥BC的是( )
 如图,下列条件能判定AD∥BC的是( )
如图,下列条件能判定AD∥BC的是( )| A. | ∠C=∠CBE | B. | ∠C+∠ABC=180° | C. | ∠FDC=∠C | D. | ∠FDC=∠A |
20.某不等式的解集x≤-1在数轴上的表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
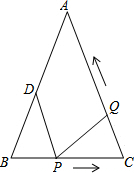 如图,已知△ABC中,AB=AC=10cm,BC=8cm,D为AB的中点,点P在线段BC上由B点出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为ts.
如图,已知△ABC中,AB=AC=10cm,BC=8cm,D为AB的中点,点P在线段BC上由B点出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为ts.