题目内容
15.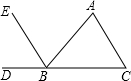 如图,能判定EB∥AC的是( )
如图,能判定EB∥AC的是( )| A. | ∠C=∠ABE | B. | ∠A=∠EBD | C. | ∠C=∠ABC | D. | ∠A=∠ABE |
分析 在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答 解:A、∠C=∠ABE不能判断出EB∥AC,故A选项不符合题意;
B、∠A=∠EBD不能判断出EB∥AC,故B选项不符合题意;
C、∠C=∠ABC只能判断出AB=AC,不能判断出EB∥AC,故C选项不符合题意;
D、∠A=∠ABE,根据内错角相等,两直线平行,可以得出EB∥AC,故D选项符合题意.
故选:D.
点评 考查了平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知一次函数y=(b-9)x+b+4的图象经过第一、二、四象限,则b的值不可能为( )
| A. | -3 | B. | 0 | C. | 7 | D. | 12 |
3.下列各式中,计算正确的是( )
| A. | 3$\sqrt{3}$+3=6$\sqrt{3}$ | B. | $\frac{1}{7}$$\sqrt{7}$=1 | C. | $\sqrt{8}$÷$\sqrt{2}$=4 | D. | $\sqrt{2}$×2$\sqrt{2}$=4 |
10. 如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
 如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
如图,正方形ABCD的边长为8,点M在边DC上,DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )| A. | 10 | B. | 8$\sqrt{2}$ | C. | 2$\sqrt{17}$ | D. | 8 |
20.要使分式$\frac{x+2}{x-3}$有意义,则x的取值应满足( )
| A. | x≠-2 | B. | x≠3 | C. | x=-2 | D. | x=-3 |
7.2016年4月30日至5月2日,河北省共接待游客1708.3万人次,实现旅游收入106.5亿元,旅行社的小王想了解某企业员工个人的旅游年消费情况,他随机抽取部分员工进行调查,并将统计结果绘制成如表所示的频数分布表,则下列说法中不正确的是( )
| 个人旅游年消费金额x/元 | x≤2000 | 2000<x≤4000 | 4000<x≤6000 | 6000<x≤8000 | 8000<x≤10000 |
| 频数 | 12 | 25 | 31 | 22 | 10 |
| A. | 小王随机抽取了100名员工 | |
| B. | 在频数分布表中,组距是2000,组数是5组 | |
| C. | 个人旅游年消费金额在6000元以上的人数占随机抽取人数的22% | |
| D. | 在随机抽取的员工中,个人旅游年消费金额在4000元以下的共有37人 |
4.如图图形中哪个是正方体的表面展开图?( )
| A. |  | B. |  | C. |  | D. |  |
5.为庆祝“六一”儿童节,某班学生准备分组外出活动,若每组8人,则余下2人;若每组9人,则少5人,求该班人数x和应分成的组数y,依题意得方程组为( )
| A. | $\left\{\begin{array}{l}{8y=x+2}\\{9y+5=x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{8y+2=x}\\{9y=x-5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{8y=x-2}\\{9y=x+5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{8y=x+2}\\{9y=x+5}\end{array}\right.$ |